Carbohydrates
D and L Notation For Sugars
Last updated: February 18th, 2025 |
The D- And L- Notation For The Absolute Configuration Of Sugars And Amino Acids
The terms D- and L- are often found in front of the names of sugars and amino acids. What do they mean?
- D- and L- is a way of describing the absolute configuration of molecules that pre-dates the (R,S) CIP system.
- D- and L-is an old but still-convenient shorthand for saying that molecules are enantiomers. e.g. D-glucose and L-glucose are non-superimposable mirror images without having to write out a long IUPAC name with lots of (R) and (S) descriptors.
- Most natural sugars are D- and most natural amino acids are L- .
- One method for determining whether a molecule is D- or L- by looking at the Fischer projection of a molecule. If the -OH (-NH2 for amino acids) on the bottom-most chiral center is on the right-hand side of the Fischer projection, the molecule is “D“. If it is on the left-hand side, the molecule is “L”.
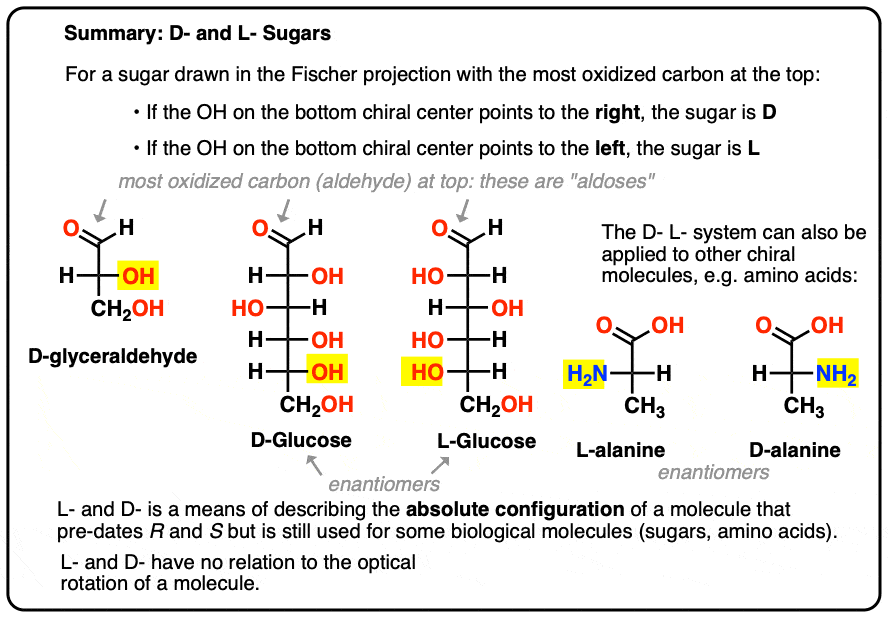
Table of Contents
- D- and L- Provides A Quick Shorthand For Designating Enantiomers
- Why Do We Bother With This Ancient Nomenclature?
- The L- And D- System For Assigning “Absolute Configuration”
- Four-Carbon Aldehyde D- and L- Sugars (Aldotetroses)
- Five-Carbon Aldehyde D- and L- Sugars (Aldopentoses)
- Six-Carbon Aldehyde D- and L- Sugars (Aldohexoses)
- But Wait – There’s More! (Amino Acids)
- Summary: D- and L- Notation For Sugars and Amino Acids
- Notes
- Quiz Yourself!
- (Advanced) References and Further Reading
1. D- And L- Provides A Quick Shorthand For Designating Enantiomers
D- and L- notation provides a quick shorthand for designating enantiomers.
D-Glucose is the enantiomer of L-Glucose, for example. As L-Alanine is the enantiomer of D-Alanine.
It is assigned as follows. For a sugar drawn in the Fischer projection with the most oxidized carbon at the top (i.e. aldehyde or ketone)
- if the OH on the bottom chiral centre points to the right, it is referred to as D-
- if the OH on the bottom chiral centre points to the left, it is referred to as L- .
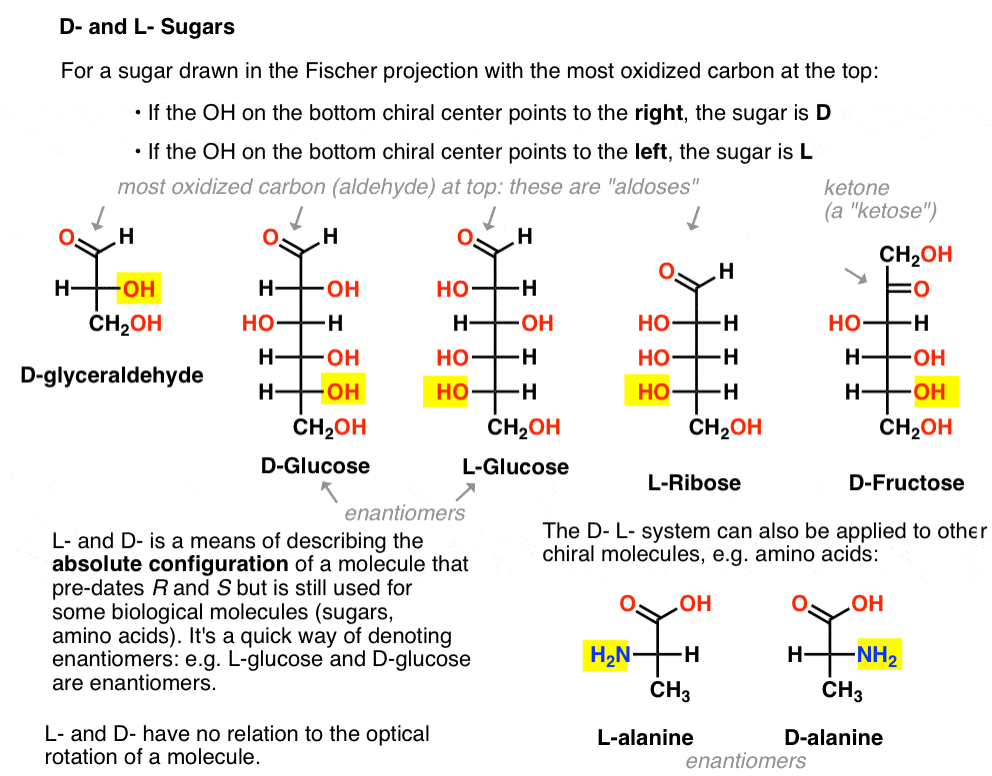
This terminology can also be applied to amino acids: see L- and D- alanine in the picture above.
2. Why Do We Bother With This Ancient Nomenclature?
You might justifiably ask: don’t we already have a system for assigning absolute configuration [the Cahn-Ingold-Prelog rules (i.e. R and S) ]? Why do we need a new system?
The D-L system isn’t a new system, folks. It’s the old system – it predates Cahn-Ingold-Prelog.
The D-L system is literally a remnant of the horse-and-buggy era, dating back to Emil Fischer’s work on carbohydrates in the late 1800s – a time when organic chemists had no way to determine the absolute configuration of stereocenters, which only became possible in 1951 (thx, Bijvoet).
So why does it still get used? Shouldn’t it be consigned to the dustbin of history, along with slide rules, 8-track cassettes, and 5 ¼” floppy disks?
Well, there are thriving communities in parts of rural America where horse-drawn carriages persist – if you know where to look. (Maybe someday there will be communes where people only use 1970s and 1980s computer technology?)
Likewise there is a pocket of organic chemistry where D-L system still finds use, and that is specifically in the realm of sugars and amino acids.
This not a revolt by Amish chemists against the modern evils of the CIP system, by the way. There are at least 3 good reasons, in the specific case of sugars and amino acids, for using L- and D- :
- Brevity. D-glucose is a heck of a lot faster to write and say than (2R,3S,4R,5R)2,3,4,5,6-pentahydroxyhexanal. The L-/D- system allows for the configuration of a molecule with multiple chiral centers to be summarized with a single letter (plus its common name, of course – thanks to Noel for the reminder)
- More brevity. It happens to be a quick way of referring to enantiomers. The enantiomer of L-glucose is D-glucose. The enantiomer of L-tryptophan is D-tryptophan. And while we could use the (+)- or (–)- prefixes to differentiate the two enantiomers of glucose and other sugars, the sign of optical rotation can vary with solvent, temperature, concentration, and other factors which makes it less than ideal. Plus, L- and D- refer specifically to absolute configuration, while (as we noted previously) there is no simple relationship between the sign of optical rotation and configuration.
- It turns out that most naturally occurring sugars are D-, and most naturally occurring amino acids are L- . There is a tremendous amount of information compressed in that statement, and there is no competing system (R/S, +/–) which could replace the L- and D- with a single character. Note 1
It bears repeating: with sugars and amino acids, L- and D- can be useful designations. For other molecules, you can largely forget about it. [(Some poor soul assigned naturally occurring morphine as D-. Give me R and S designations any day.]
So what is this D-/L- system, and how do these terms relate to structure?
Join me as we travel back through time…
3. The L- And D- System For Assigning “Absolute Configuration”
Emil Fischer began studying carbohydrates in the late 1880’s. It was known by that time (via Van’t Hoff) that carbon was tetrahedral, and it was also known that molecules containing a carbon with four different substituents could rotate plane-polarized light (e.g. Pasteur). What wasn’t known was the absolute configuration of any of the chiral molecules – what we’d refer to today as their “R” and “S” configurations.
The simplest carbohydrate [Cn(H2O)n] containing a chiral center is glyceraldehyde, C3H6O3. Glyceraldehyde has three carbons; making it a “triose”. The most oxidized carbon in glyceraldehyde is an aldehyde, which also makes it an “aldose”. [These terms are often combined: “aldotriose” refers to a 3 carbon sugar containing an aldehyde. ]
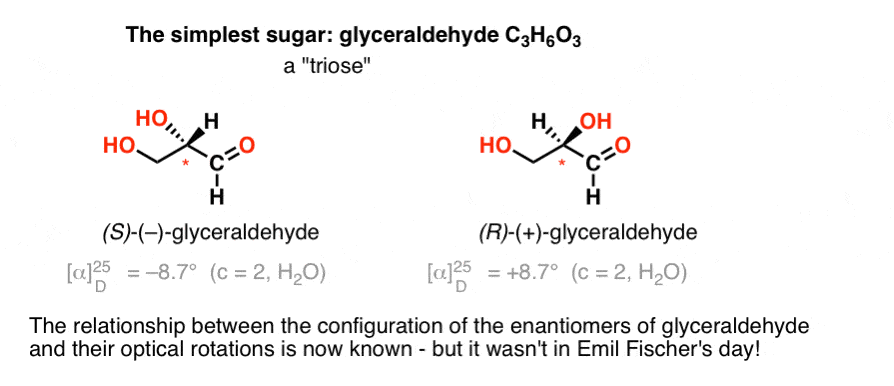
In 1888, the two enantiomers of glyceraldehyde [(+)- and (–)] had been isolated and characterized. But since there’s no simple correlation between the configuration of a chiral centre and the direction in which it rotates plane-polarized light, Emil Fischer had no way of tying back the optical rotation of (+)- and (–)-glyceraldehyde to the absolute configuration of the atoms around the chiral centre.
Using today’s terminology, he had no way of knowing whether (–)-glyceraldehyde was (R) or (S).
Lacking this key piece of information, Fischer chose to guess.
The guess, which turned out to be correct, was that (–)-glyceraldehyde had the configuration we now call S, and that (+)-glyceraldehyde has the configuration we now call R.
Of course, Cahn, Ingold, and Prelog hadn’t been born yet, and the CIP system would only be developed after Bijvoet’s work in 1951. So Fischer developed his own nomenclature.
Drawing glyceraldehyde in what would later be called the Fischer projection, he assigned the configuration on the left to (–)-glyceraldehyde, and called it L- (short for Latin laevo ). He then assigned the configuration on the right to (+)-glyceraldehyde, and called it D- (for Latin dextro ).

Why is this so important?
Assigning the absolute configuration for L- and D- glyceraldehyde was a bit like assigning the Prime Meridian (0° longitude) to the Royal Observatory in Greenwich, England. Just like longitude of every other place on earth could then be determined relative to that point if their relative distances were known, the absolute configuration of every other stereocenter could then be determined if its configuration relative to L- or D- glyceraldehyde was known.
That might not be the clearest analogy. So let’s look at the 4-carbon sugars for another example.
4. Four Carbon Aldehyde D- and L- Sugars (Aldotetroses)
Once the absolute configurations of L- and D- glyceraldehyde were proposed, the absolute configurations of other chiral compounds could then be established by analogy (and a lot of chemical grunt work).
It’s not crucial for today, but for an example of this kind of reasoning, see this [Note 2]. [We will revisit it when we write about the Fischer Proof for the structure of glucose.]
Back when the concept of chiral centers was being introduced, you likely learned that a molecule with n chiral centers will have 2n stereoisomers (as long as there are no meso compounds).
There are two four-carbon aldoses, threose and erythrose. They each have two chiral centers. Each exist as a pair of enantiomers (L- and D- ) giving four stereoisomers in total.
Here they are. The important thing to note in the figure below is that the L-family of sugars has the OH group of the bottom chiral carbon on the left, and the D-family has the OH group of the bottom chiral carbon on the right (highlighted).
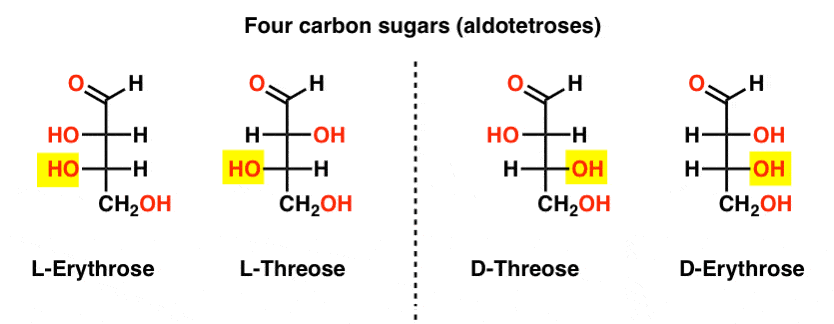
See how L-Erythrose and L-Threose build on the stereocenter established in L-glyceraldehyde (highlighted), and D-Erythrose and D-Threose build on the stereocenter established in D-glyceraldehyde (highlighted).
Sugars are built up a little like the binary system; you can think of each stereocenter is a “bit” that can have one of two values. The configuration of L-erythrose and L-threose only differs at one stereocenter. If we were to flip the position of H and OH, we’d get the other. This relationship has a name that you might see sometimes: two molecules that have the opposite configuration at just one stereocenter are called epimers, particularly when one of the atoms attached to the stereocenter is a hydrogen (H).
5. Five Carbon Aldehyde D- and L- Sugars (Aldopentoses)
There is a quartet of five-carbon aldehyde sugars (aldopentoses): ribose, arabinose, xylose, and lyxose, each existing as a pair of enantiomers (D- and L- ).
The most familiar name on that list should be ribose, which is the sugar backbone of ribonucleic acid (RNA).
On the left hand side in the diagram below, we have the L-aldopentoses, which all share the same configuration of the bottom stereocenter when the aldehyde is placed at the top.
Their enantiomers, the D-aldopentoses, are on the right hand side, which all share the same configuration of the bottom stereocenter (highlighted).
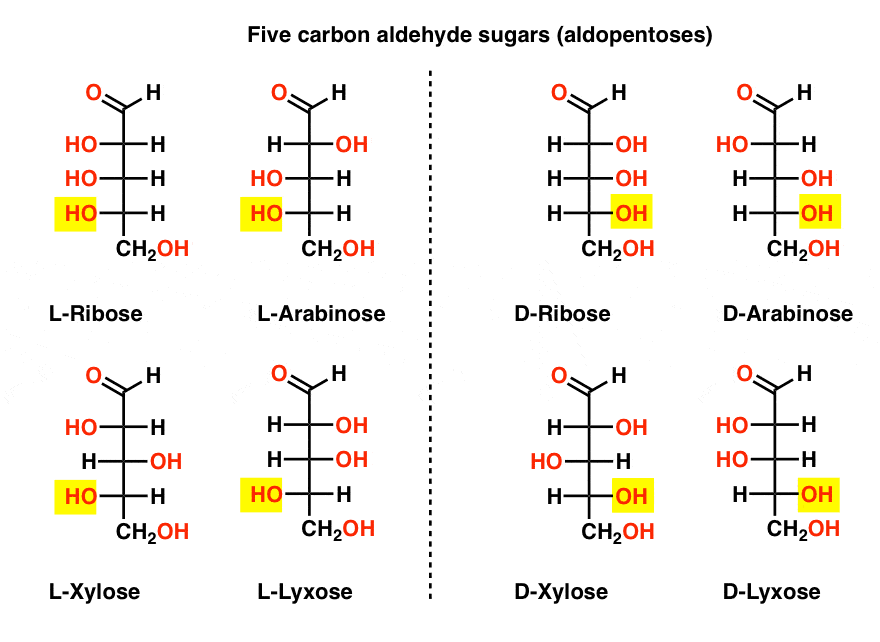
At this point we should point out that the overwhelming majority of sugars in Earth-based life forms are D- sugars, including D-ribose as the backbone of RNA. Why and how all organisms on earth ended up with D-sugars is a mystery, as one presumes that L-sugars would have worked just as well. [This has provided grist for science fiction writers such as Arthur C. Clarke, as well as a somewhat poorly received Star Trek novel. Thanks @Prof_West, @vancew, @RoseChem2 and @PeONor for the tips!]
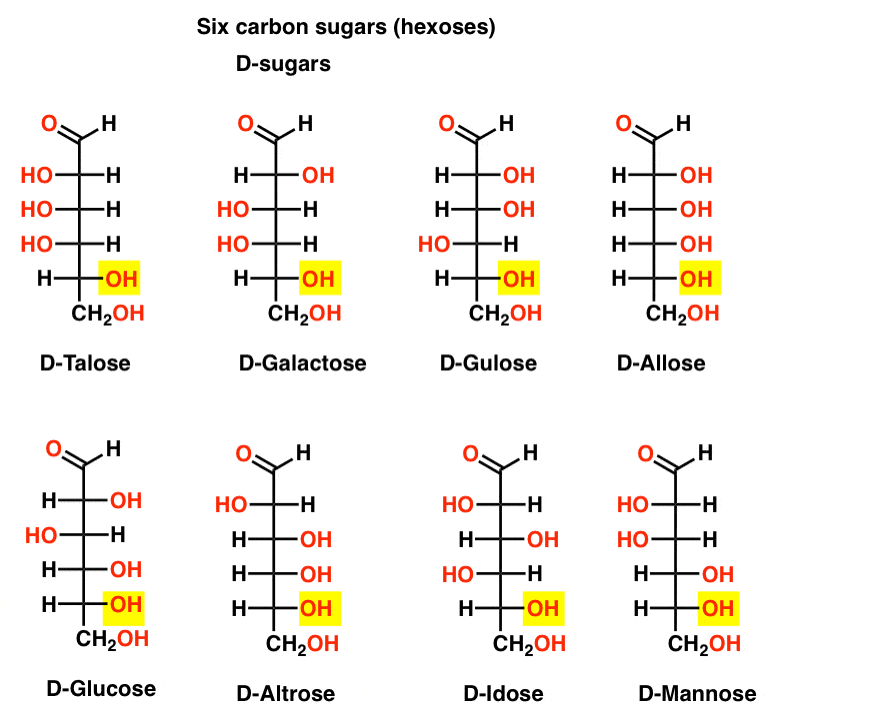
6. Six Carbon Aldehyde D- and L- Sugars (Aldohexoses)
If there are 4 aldopentoses, each as a D- L- pair of enantiomers (8 stereoisomers total) then how many aldohexoses are there?
There are 8 D-L- pairs (16 stereoisomers total). The most familiar is glucose, but you’ll likely recognize mannose and galactose. Some are rarely, if ever, found in nature (idose, anyone?).
Here are the D-aldohexoses. Note how they all have the same configuration of the bottom chiral centre – the same one we saw in D-glyceraldehyde.
In contrast to the D-sugars, the L- sugars (below) are rarely found in nature. Interestingly, L-glucose has been explored as a sugar substitute. Its taste is indistinguishable from naturally occurring D-glucose, but provides no nourishment since it cannot be broken down by our (chiral) enzymes. As it turns out production is just too expensive to compete with splenda, stevia, aspartame et. al.
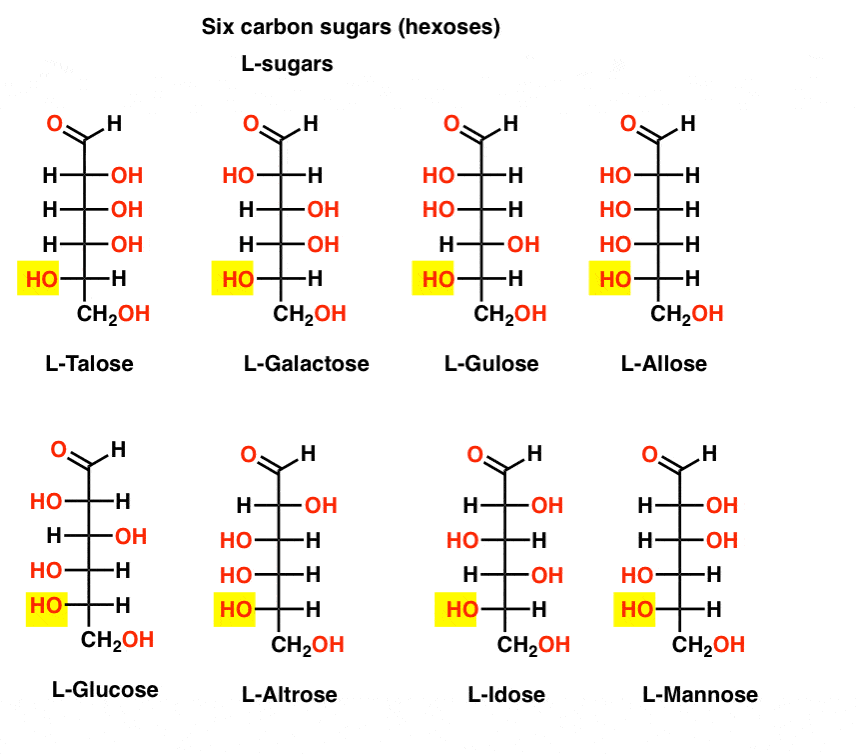
OK, that’s enough. Seven-carbon sugars have been made (aldoheptoses) but they’re not biologically significant.
7. But Wait – There’s More! (Amino Acids)
If you draw amino acids in the Fischer projection with the most oxidized group at the top (the carboxylic acid) then you can also assign L- and D-.
Of the 19 chiral amino acids that are incorporated into proteins (proteinogenic is the proper term) are all L- . (Glycine is achiral, so D- and L- doesn’t apply). Some D- amino acids are naturally occurring, but they are rare (mostly found in bacteria, with the notable exception of platypus venom) and are not coded by mRNA.
Interestingly, although all 19 chiral amino acids are L- , only 18 of the 19 are (S). What’s the exception?
(This is good organic chemistry bar trivia).
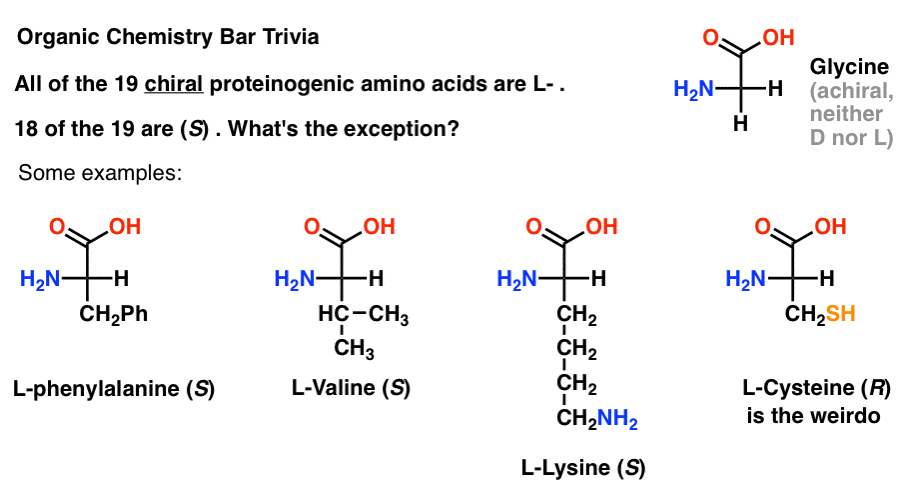
Cysteine is the weirdo.
(Bonus points if you also said selenocysteine … nerd).
8. Summary: D- and L- Notation For Sugars And Amino Acids
So that’s the D- L- system for assignment of absolute configuration. It works well for sugars since they can be built up so systematically (like the binary system). It’s also useful for amino acids. The key point is just to look at the bottom stereocenter while it’s drawn in the Fischer projection. Right? D. Left? L.
Of course, sugars are not always so helpfully drawn in Fischer projections – they form rings. We’ll write about determining D- and L- in cyclic sugars in a future post.
All I have to say is, thank whatever deity you choose to believe in that Fischer’s guess turned out to be correct. It would be an enormous pain in the ass to sift through 70+ years of the chemical literature knowing that the wrong configuration had been assigned to all the sugars and amino acids.
Thanks to Thomas Struble for assistance with this post.
Notes
Related Articles
Note 1.“the penultimate stereocenter in most chiral sugars is R, while the stereocenter in most amino acids is S” doesn’t have quite the same ring, especially since cysteine is R.
Note 2. Here’s a thought experiment for determining the relative configurations of erythrose and threose. (I say “thought experiment” because I don’t want to include specific reagents, which could be distracting)
If one starts with pure (+)-erythrose and oxidizes the primary alcohol to an aldehyde using known methods, one obtains a compound lacking any optical rotation. The same is true for (–)-erythrose, which returns a completely identical compound. From this it can be deduced that the structure of the new compound must be such that the molecule has an internal mirror plane (i.e. it’s meso). [Oxidizing the compound further to a di-carboxylic acid would produce meso-tartaric acid, whose structure was known].
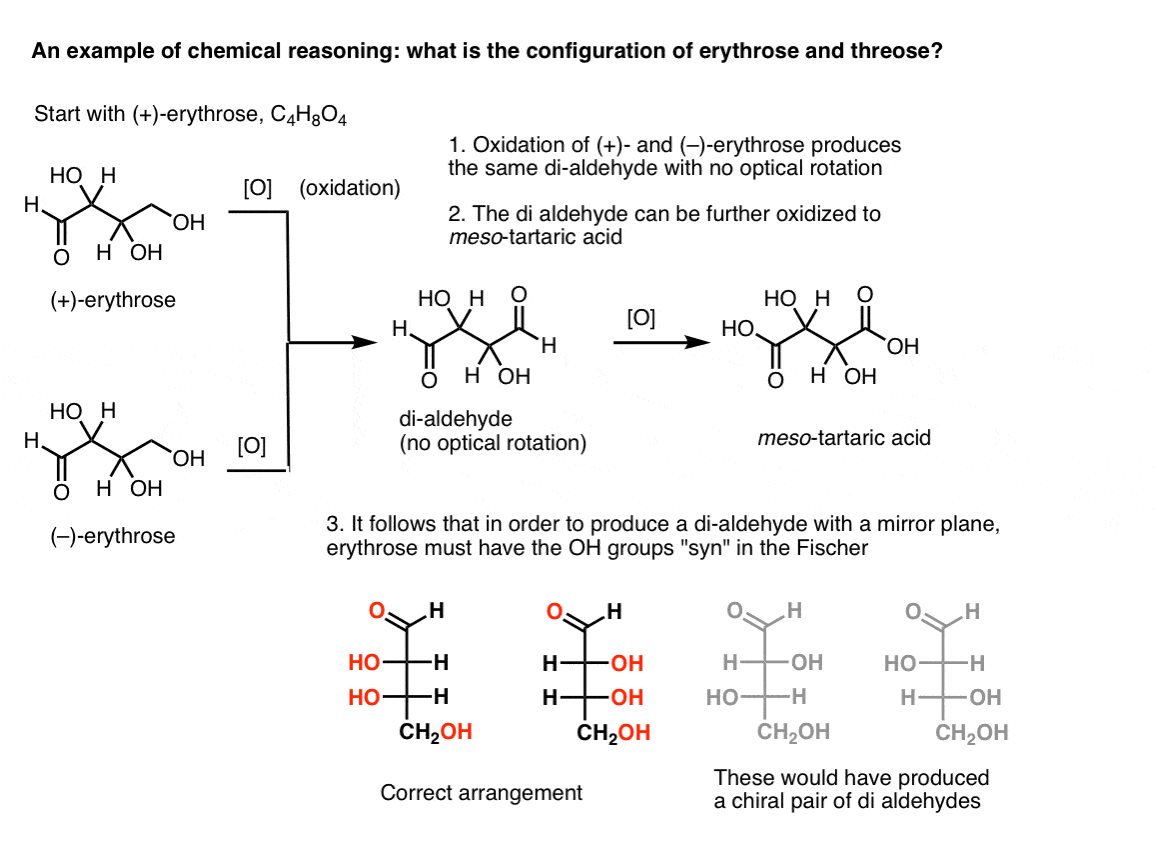
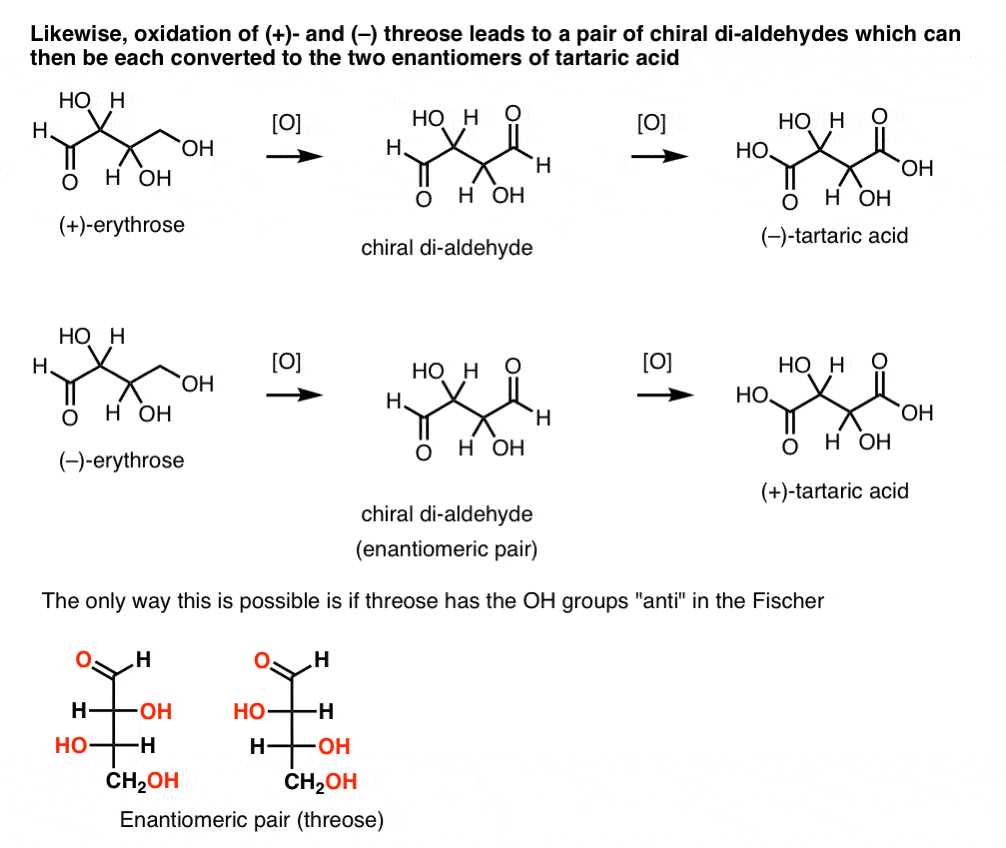
In contrast, performing the same operation on (+)-threose results in a di-aldehyde that maintains optical rotation. A compound with equal and opposite optical rotation is formed by performing the same operation on (–)-threose. These two compounds are enantiomers. In order for that to be true, the relative orientation of the hydroxyl groups in threose must be anti. These compounds can be oxidized further to produce, respectively, (–)- and (+)- tartaric acid.
The same reasoning can be used in the opposite direction (reduction). For instance either (+)- or (–)- erythrose can be reduced to the tetra-ol erythritol, which is meso.
Likewise, reduction of (+)- and (–) threose results in an enantiomeric pair of tetra-ols, threitol.
From these facts we can deduce the relative orientation of the OH groups.
[A side note: in older literature, the terms erythro- and threo- are sometimes used to describe the relationship between pairs of diastereomers with two chiral centers. Nowadays we tend to use syn and anti instead].
Quiz Yourself!

Become a MOC member to see the clickable quiz with answers on the back.

Become a MOC member to see the clickable quiz with answers on the back.

Become a MOC member to see the clickable quiz with answers on the back.

Become a MOC member to see the clickable quiz with answers on the back.

Become a MOC member to see the clickable quiz with answers on the back.
(Advanced) References and Further Reading
- Über die Bezeichnung von optischen Antipoden durch die Buchstaben d und l
Emil Fischer
Ber. 1907, 40 (1), 102-106
DOI: 10.1002/cber.19070400111
This is the famous paper where Prof. Emil Fischer (arbitrarily!) assigned (-)-glyceraldehyde the L-stereochemistry. - Syntheses in the Purine and Sugar Group
Emil Fischer
Nobel Lecture, 1902
Fischer’s Nobel Lecture, where he talks about his work not just in carbohydrates, but also in purines, of which compounds like caffeine and theobromine are members. Prof. Fischer predicts the rise of energy drinks (e.g. Red Bull), stating, “with the exercise of a little imagination the day can be foreseen when beans will no longer be required to make good coffee: a small amount of powder from a chemical works together with water will provide a savoury, refreshing drink surprisingly cheaply”. - Determination of the Absolute Configuration of Optically Active Compounds by Means of X-Rays
BIJVOET, J., PEERDEMAN, A. & van BOMMEL, A.
Nature 1951, 168, 271–272
DOI: 1038/168271a0
The famous paper that proved, using X-ray structural analysis, that “Emil Fischer’s convention, which assigned the configuration of Fig. 2 to the dextrorotatory acid, appears to answer to reality”. - Emil Fischer’s discovery of the configuration of glucose. A semicentennial retrospect
C. S. Hudson
Journal of Chemical Education 1941, 18 (8), 353
DOI: 10.1021/ed018p353
An early review that covers Prof. Emil Fischer’s work in carbohydrate chemistry. - Emil Fischer’s Proof of the Configuration of Sugars: A Centennial Tribute
Frieder W. Lichtenthaler
Angew. Chem. Int. Ed. 1992, 31 (12), 1541-1556
DOI: 10.1002/anie.199215413
A very readable review from 1992 that covers Prof. Fischer’s work in carbohydrate chemistry and goes in-depth into the stereochemical assignments of carbohydrates.
Why only look OH at the bottom so classify into D/L, why not to take and compare all of the OH attached?
Even we can write hydroxy into OH or HO which One is correct, most of the time on fischer projection is applicable is that appropriate?
Thanks with regards for your answers.
Hello,
How do we determine d and l configuration in cyclic sugars ?
For a hexose, you’re looking at the C-5 stereocenter which is (R) for the D-sugars. When the hexose is drawn as a nice six-membered ring with the C1-c2-c3-c4- numbered clockwise (99% of cases, i.e. anomeric C-1 carbon on the right) if the C-5 CH2OH points up, it’s D and if it points down it’s L.
Things get more complicated if the hexose is drawn in its pyranose form. You need to determine if C-5 is (R) or (S).
For pentoses, you have to look at the C-4 chiral center.
Assuming sufficiently advanced technology, if humans were to be artificially created but with every chiral molecules in its opposite enantiomer to “normal”, would the percentages of left and right handed people be reversed in such a population?
I’m not aware that we fully understand what makes humans left- or right-handed in the first place, so your guess is as good as mine.
Why is it the last asymmetric carbon that determines the D/L configuration?
Good question. It’s a naming convention, so at some level it becomes, “because X says so! ” rather than a physical explanation.
However, it is wiser than at least one alternative. If it were the asymmetric carbon *nearest* the aldehyde that determines D/L , that would pose serious problems as the C-2 carbon’s configuration can change through “epimerization” (i.e. formation of an enol/enolate followed by protonation). As “D” and “L” denote “absolute configuration” and therefore define a pair of enantiomers, this would be a bad protocol if changing one chiral center (e.g. flipping C-2 of glucose to give mannose) resulted in switching the name from D- to L- .
I don’t know if this answers your question, feel free to drill down to something more specific.
What do you think of chemical vendors selling you “D(+)sucrose”?
(Yeah, google it, there’s lots of this happening.)
D or L isomerism will be determined by the amino group
Yes, that is correct.
For the amino acid threonine, would the D or L be determined by the position of the hydroxyl group rather than the amino group on the second chiral center (farther from the carboxylate)? Similarly, for isoleucine, would D or L be determined by the methyl/ethyl group farther from the carboxylate than the amino group?
Hi Aaron, D or L is determined by the amino group, not the sidechain.
Amazing Work Thanks For Sharing.
Hi! I was determining the R/S configuration of L-cysteine. May I know if my understanding below correct?
Looking at the chiral carbon, the 4 groups are NH2, COOH, H and CH2SH. I assign priority #1 to NH2 and #4 to H. Then between the remaining groups, the carbon in COOH is attached to O,O,O while the carbon in CH2SH is attached to S,H,H. I do not sum up the Ar of the atoms when assigning priority. S,H,H is given a higher priority than O,O,O by virtue of S atom alone having higher Ar than O atom.
Therefore, CH2SH is given priority #2 while COOH is given #3. Am I right?
Your reply would be much appreciated!
You are absolutely correct, Gwen.
Why all elible sugar are in D form and not in L form?
Well, that’s a very deep question, and likely a “frozen accident” owing to the quirks of how life evolved on Earth. We just don’t know.
Isn’t glucose and drawn incorrectly?
Not in the first figure but towards the end.
At the end, L-glucose is drawn, which is the enantiomer of D-glucose.
Question, what if you flip the Fischer projection of the molecule, phenylalanine for instance. would the D/L- system still be applicable or…?
The rule is you must have the most oxidized carbon at the top of the Fischer. So the Fischer must be drawn with the carboxylic acid at the top. D- and L- still applies for phenylalanine.
What if there’s one amine group and one -OH group? How will we name it giving priority to
-OH or -NH2 ?
I’m not sure what you mean. You’d have to provide an example. A carbon connected to both -OH and -NH2 would not be very stable (an aminal)
Great post. Just a minor correction: “The L-/D- system allows for the configuration of a molecule with multiple chiral centers to be summarized with a single letter.” For aldohexoses, the letter itself just narrows down the stereochemistry to one of 8 configurations; it’s the letter plus the configuration prefix (“gluco”) that pinpoints the specific epimer.
I quite like the D/L system. It reminds us that all tetrahedral stereochemistry must be defined relative to something. With CIP it’s relative to an ordering of attachments by some rules in a book. With D/L it’s relative to the ordering in D/L-glyceraldehyde. With various file formats for molecules, it’s typically relative to the order of the atoms in the file.
Thanks Noel, for the correction and the comment.