Home / Isoelectric Points of Amino Acids (and How To Calculate Them)
Carbohydrates
Isoelectric Points of Amino Acids (and How To Calculate Them)
Last updated: February 5th, 2025 |
Isoelectric Points Of Amino Acids (And How To Calculate Them)
The isoelectric point of an amino acid is the pH at which it bears no net charge.
- Amino acids have an amino group and a carboxylic acid
- Although they are often drawn in their neutral form, in aqueous solution at pH 7 (physiological pH) their structure is more accurately described as a “zwitterion” (an internal salt) – the product of an acid-base reaction between the carboxylic acid and the amine.
- The zwitterionic form has two point charges but has a net charge of 0.
- In practice, the charges on an amino acid only balance out to zero at one specific pH value, called the isoelectric point pI. At this pH, the amino acid will not migrate in an applied electric field.
- For amino acids with neutral sidechains, the pI can be calculated by averaging the pKa values of the carboxylic acid and ammonium groups
- For amino acids with acidic sidechains, the pI can be calculated by averaging the pKa values of the two most acidic groups
- For amino acids with basic sidechains, the pI can be calculated by averaging the pKa values of the least acidic groups
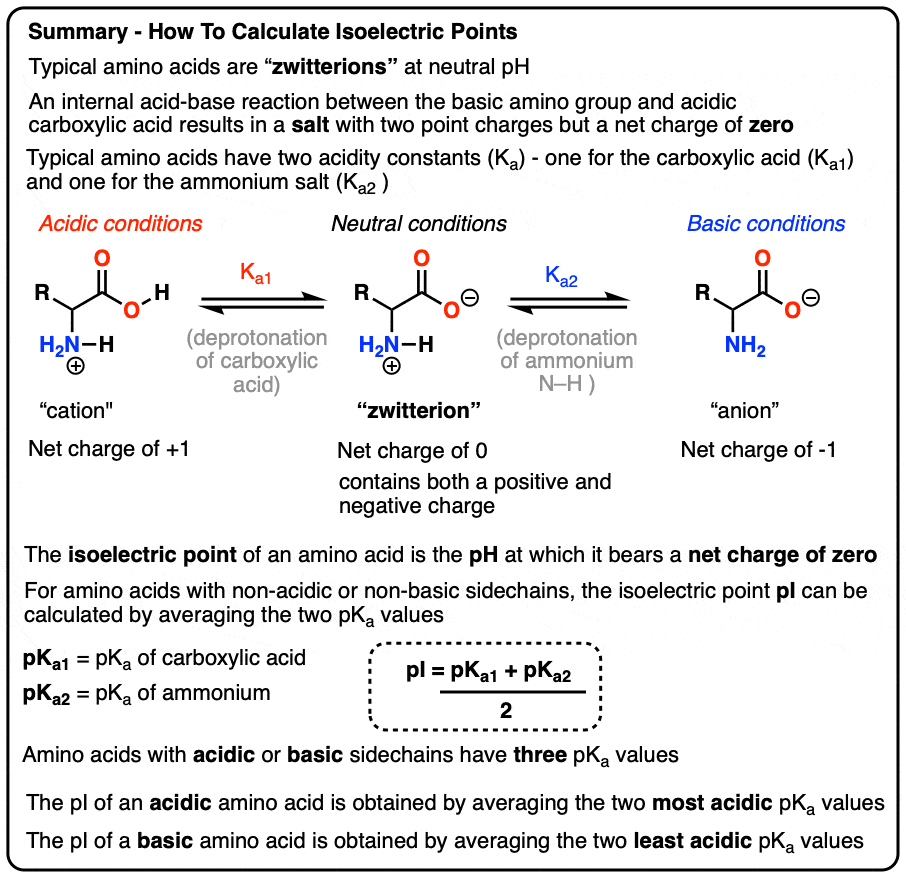
Table of Contents
- Amino Acids as Zwitterions
- The Isoelectric Point, pI, Is the pH At Which Negative and Positive Charges are Balanced
- Calculating Isoelectric Point pI from pKa Values
- pI Calculations for Amino Acids With Acidic Side Chains
- pI Calculations for Amino Acids With Basic Side Chains
- Summary
- Notes
- Quiz Yourself!
- (Advanced) References and Further Reading
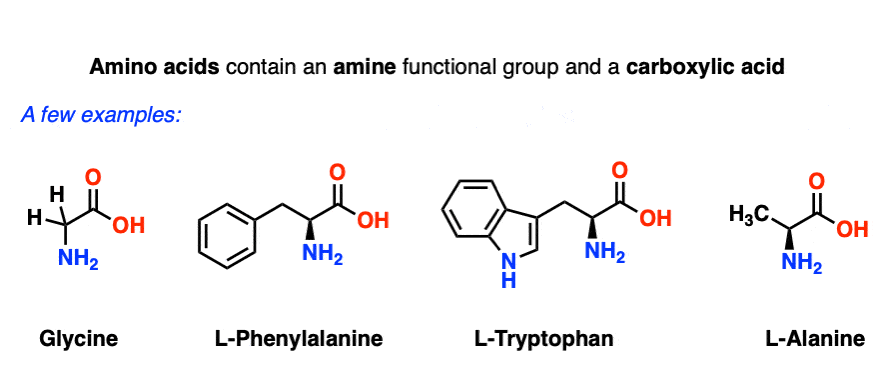
1. Amino Acids As Zwitterions
Amino acids contain a carboxylic acid and an amino group. We often like to draw them like this:
Although simple, these drawings don’t accurately convey the physical properties of these molecules, especially under physiological conditions.
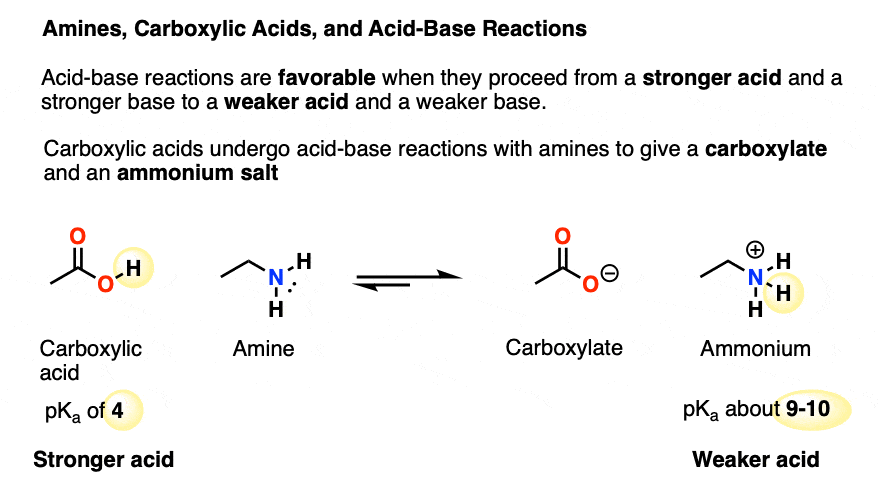
When a carboxylic acid (pH 4) is added to a solution containing an amine (R-NH2), an acid-base reaction quickly occurs, resulting in formation of the ammonium salt R-NH3(+) with a pKa of about 9.
This is a favorable equilibrium because the reaction proceeds from a stronger acid and a stronger base to a weaker acid and a weaker base. [See article: How To Use a pKa Table]
Should amino acids behave any differently than the carboxylic acids and amines we’re familiar with?
No! Amino acids are acids. They are also bases containing an amino group. The term amphoteric is often used to describe amino acids, meaning that they are capable of acting as both acids and bases.
When dissolved in water (especially when dissolved in the polar solvent water!) we should likewise expect an acid-base reaction between the carboxylic acid and the amine.
Here’s what it would look like for the simplest amino acid, glycine. The pKa of the carboxylic acid is 2.24 and the pKa of the amino group is 9.60.
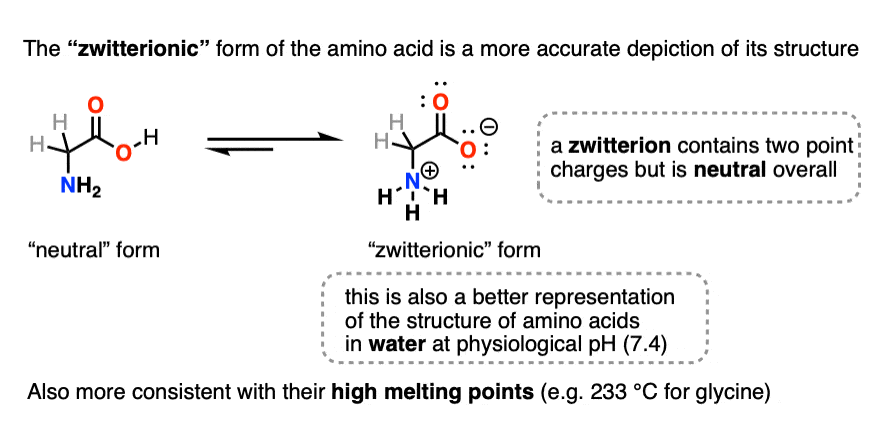
Glycine has become a salt, with a negatively charged carboxylate group and a positively charged ammonium group.
These “internal salts” are known as zwitterions. Note that, as drawn, the molecule bears no net charge since the positive and negative charges balance out.
The high melting point of glycine [233°C] and other amino acids is more consistent with this zwitterionic structure than the neutral form that is often drawn.
2. The Isoelectric Point, pI, Is The pH At Which Negative and Positive Charges Are Balanced
In practice, the zwitterionic amino acid will only have a net charge of zero at a very narrow range of pH values.
The pH at which the negative and positive charges are in balance is known as the isoelectric point.
At pH values below and above the isoelectric point, the molecule will bear a net positive or net negative charge, respectively.
It’s possible to test this by applying a sample of the amino acid to specially treated paper or gel and applying an electric field at different pH values – a technique known as electrophoresis. A molecule with a net charge of zero will not migrate in an electric field, whereas one bearing a positive or negative charge will migrate towards the cathode or anode, respectively.
Why might this be? Let’s have a look at a typical amino acid in its zwitterionic form.
The carboxylate group is a weak base, and the ammonium salt is a weak acid.
If the pH is decreased to a low enough value (e.g. pH 1) then the carboxylate salt will be protonated to give the neutral carboxylic acid, and the molecule will have a net charge of +1.
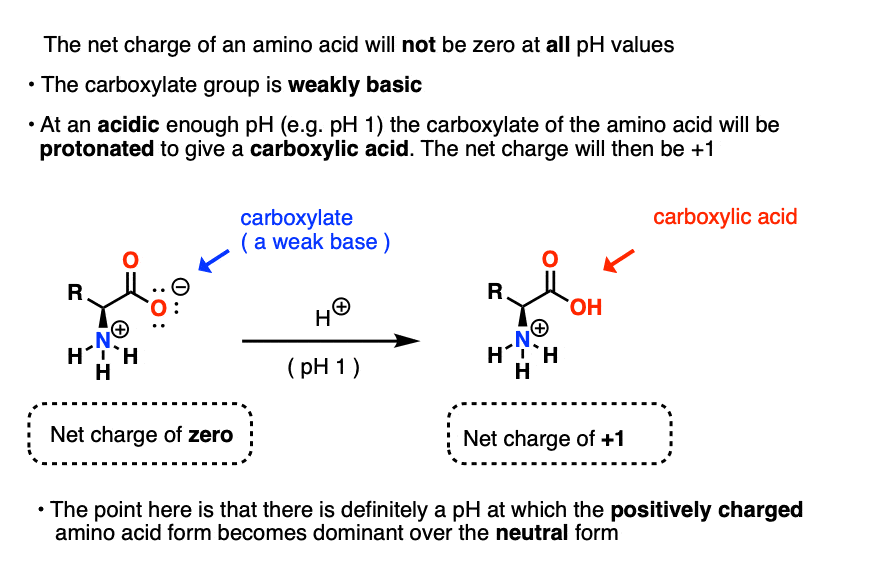
If the pH is increased to a high enough value (e.g. pH 14) then the ammonium salt will be deprotonated to give the neutral amine. The molecule will have a net charge of -1.
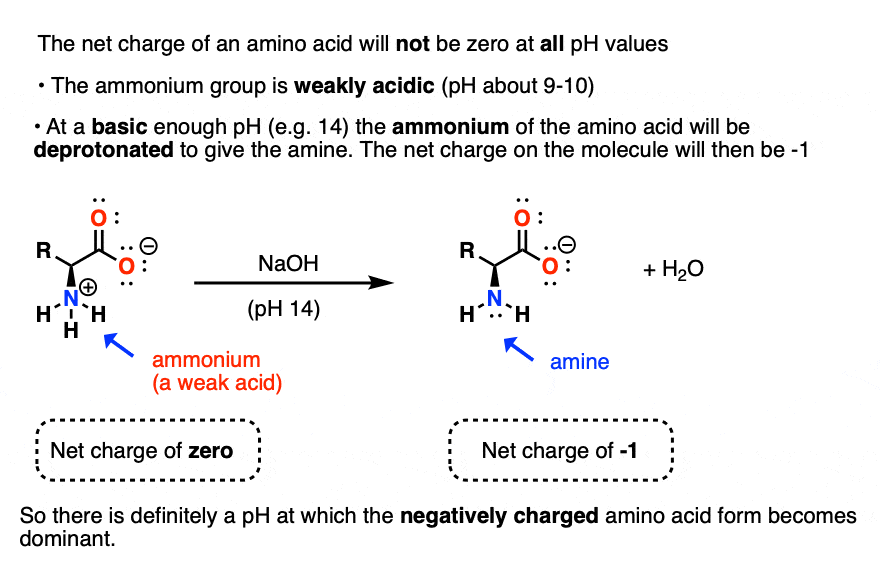
Putting all of these acid-base reactions together, from low pH to high pH we get:
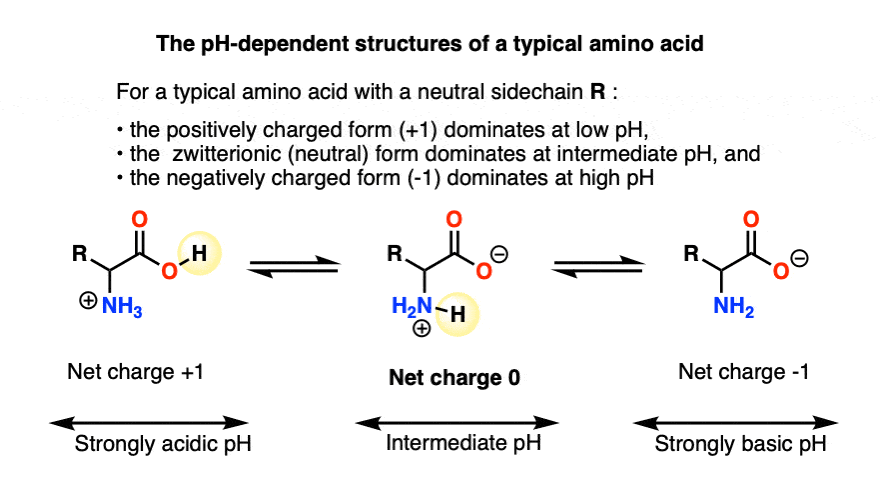
For a typical amino acid, there will be a range of pH values where the positively charged form dominates, another where the neutral form dominates, and finally one where the negatively charged one dominates.
We could even make a sketch of mol percentage versus pH, and imagine it would look something like the following.
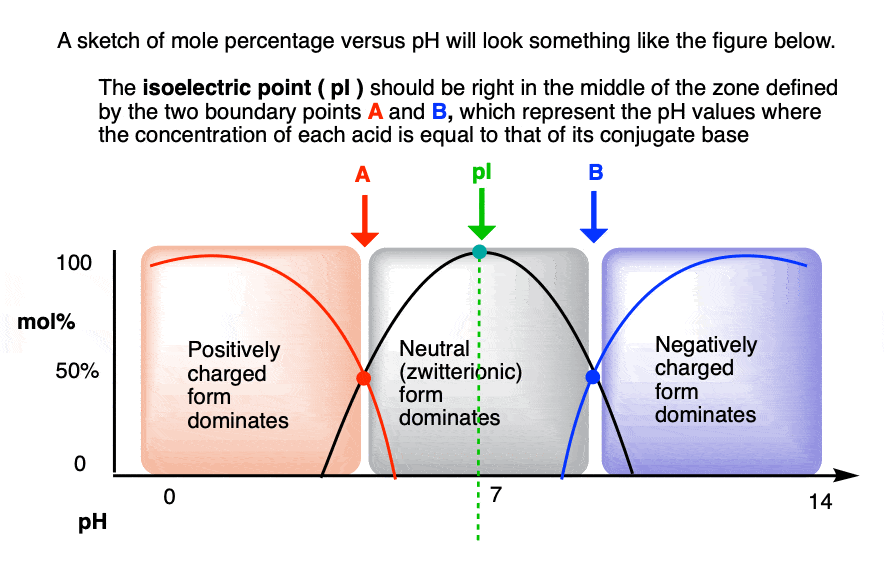
The isoelectric point, pI should be right in the middle of the two points A and B where there each acid is equal in concentration to its conjugate base.
[Note 1 – for more detailed calculations, refer to this site]
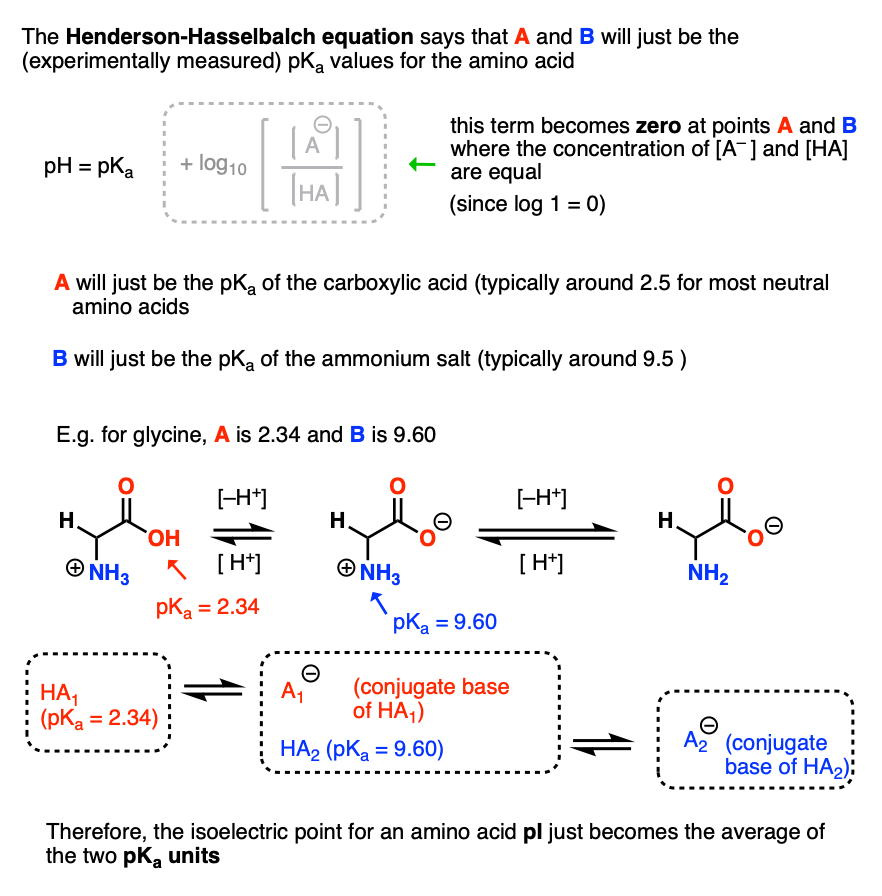
3. The Formula for Calculating Isoelectric Point, pI
If only there were some formula we could use for figuring out the pH of points A and B on the graph above, where the acid and its conjugate base are present in equal concentration.
Thankfully, our old friend the Henderson-Hasselbalch equation gives us the answer!
When an acid is present in equal concentration with its conjugate base, the pH of the solution will simply be equal to the pKa of the acid.
[For a more detailed treatment, see Note 2]
This means that the two points A and B on the sketch above correspond to the pKa values of the amino acid.
So, in order to obtain the isoelectric point, all we have to do is average these two values.
Thankfully, the pKa values for all proteinogenic amino acids have been determined experimentally.
The pKa values for glycine, for example, are 2.34 (for the carboxylic acid) and 9.60 (for the ammonium).
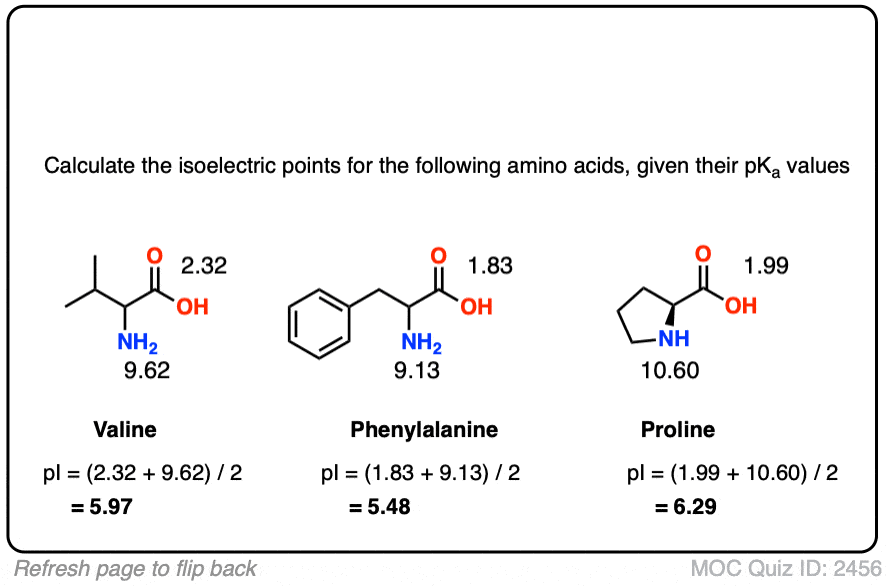
Adding the two pKa values together and dividing by 2 gives us a value of 5.97 for the isoelectric point.

Here is a table with some structures and pKa values for amino acids.
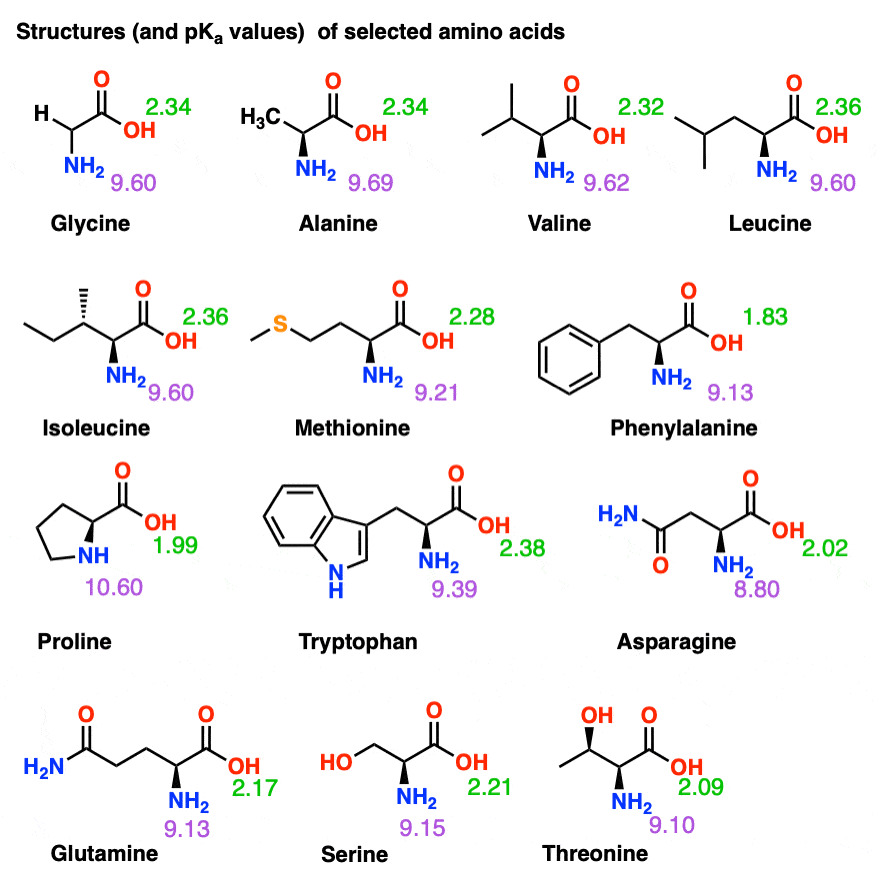
This table omits the amino acids with acidic and basic side chains, in addition to cysteine and tyrosine (all of which have 3 pKa values!).
See if you can calculate the isoelectric points.
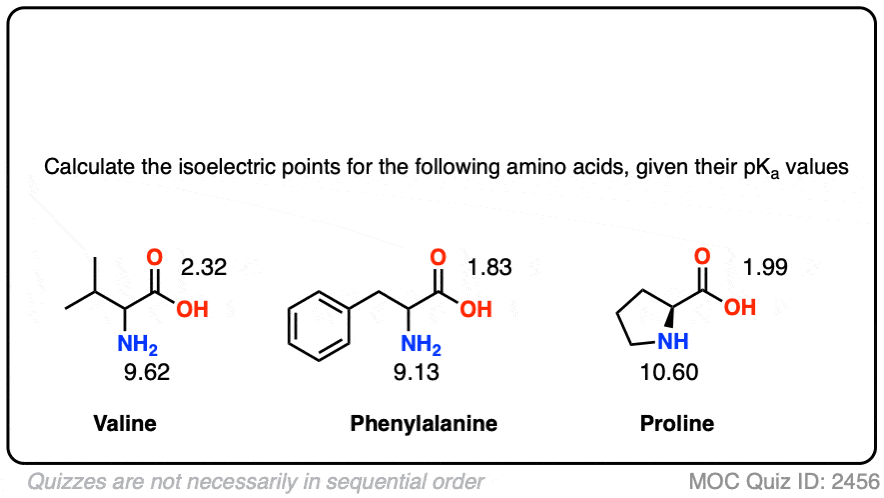 Click to Flip
Click to Flip
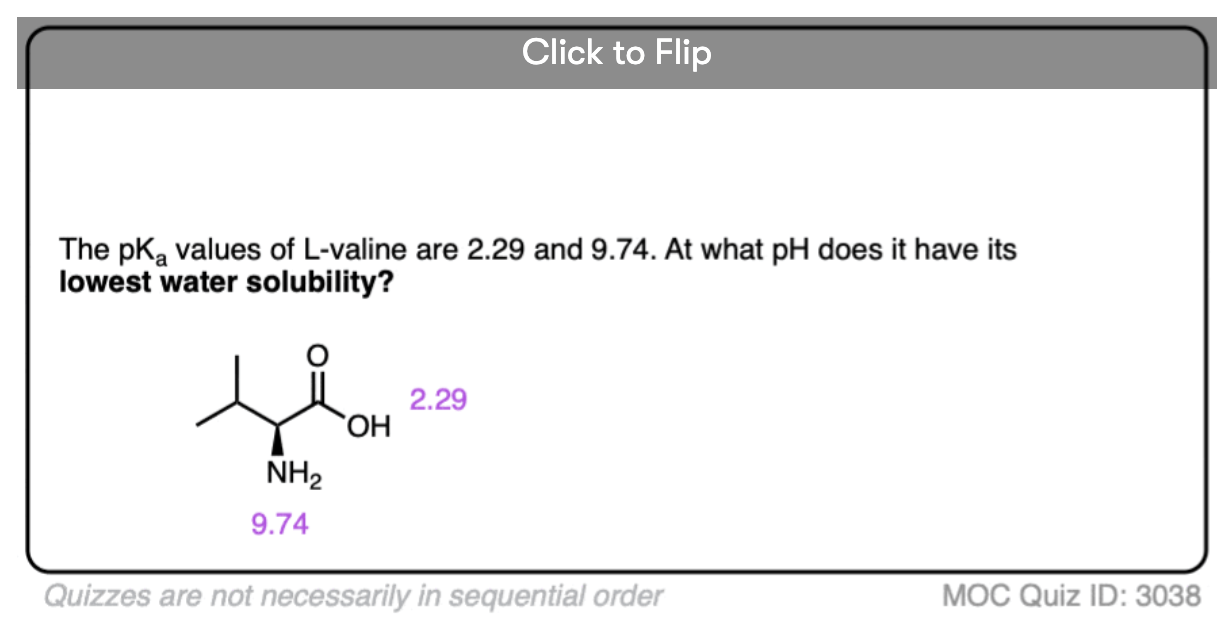
4. Acidic Side Chains
Obtaining pI through averaging the two pKa values of the amino acid is simple enough.
But what happens when the amino acid contains an acidic side chain, such as in Glutamic acid (Glu) and aspartic acid (Asp)? How will that affect the isoelectric point?
First, let’s just take a guess. Do you think the pI will become lower or higher as a result of the acidic side chain?
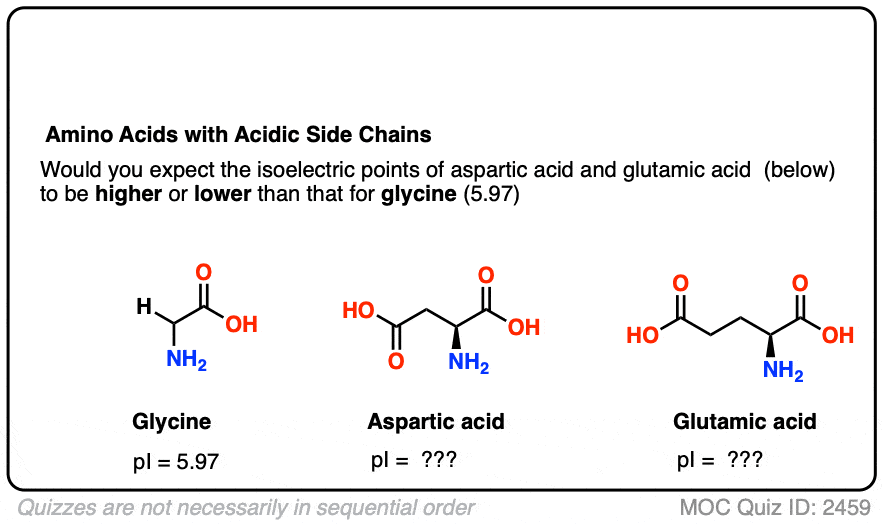 Click to Flip
Click to Flip
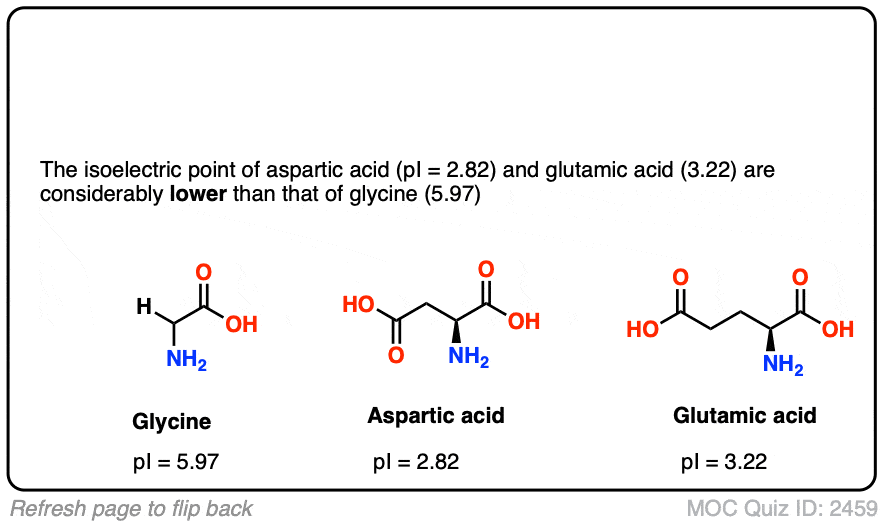
It may be helpful to walk through the changes in the molecule as we proceed from extremely low pH to high pH.
Let’s use aspartic acid as the example.
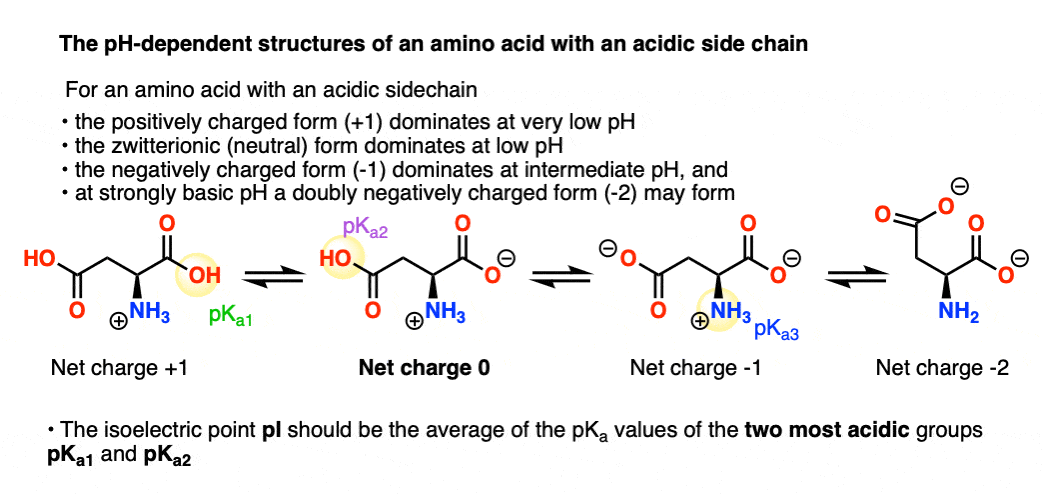
- At extremely low pH (e.g. pH 1), both carboxylic acids should be protonated along with the amino group, for a net charge of +1.
- As acidity decreases, the most acidic carboxylic acid will be deprotonated to give us the zwitterionic form (net charge = 0)
- With a further increase in basicity, the second carboxylic acid is deprotonated to give a net negatively charged form (net charge = -1)
- at very high basicity (e.g. pH 14) the ammonium will be deprotonated, giving a doubly negatively charged species (net charge = -2)
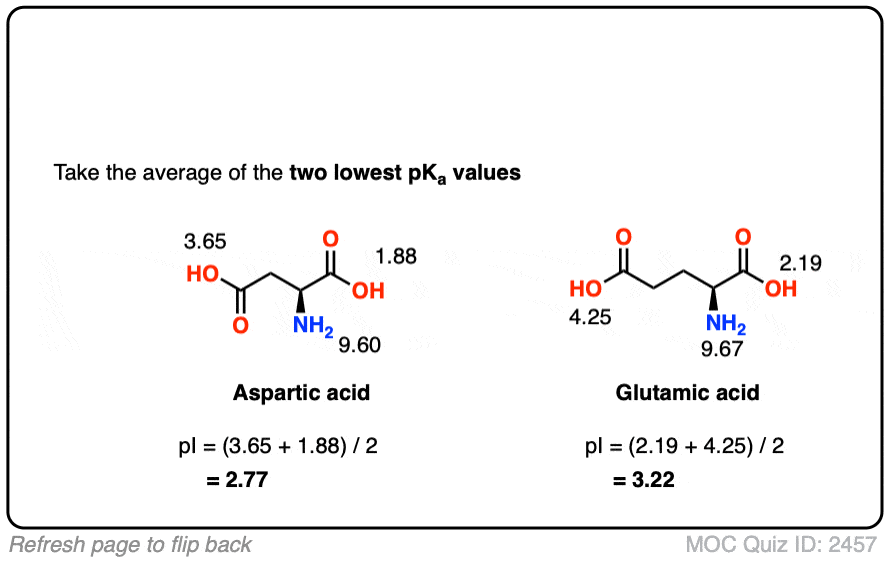
Since the net neutral species is formed through loss of a proton on the most acidic site (pKa1 = 1.88 for aspartic acid ), and destroyed through loss of a proton on the second-most acidic site (pKa2 = 3.65 for aspartic acid) the concentration of the neutral species should be at its maximum at the point midway between these two values.
See if you can calculate the pI of aspartic and glutamic acid.
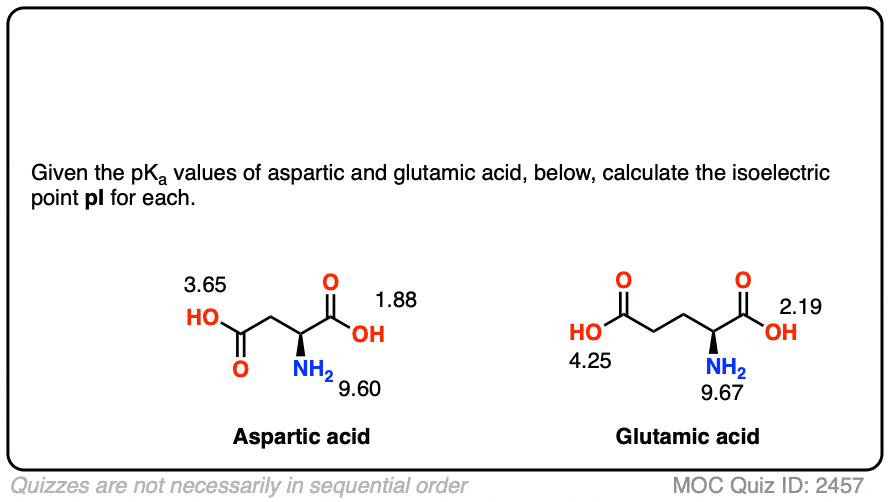 Click to Flip
Click to Flip
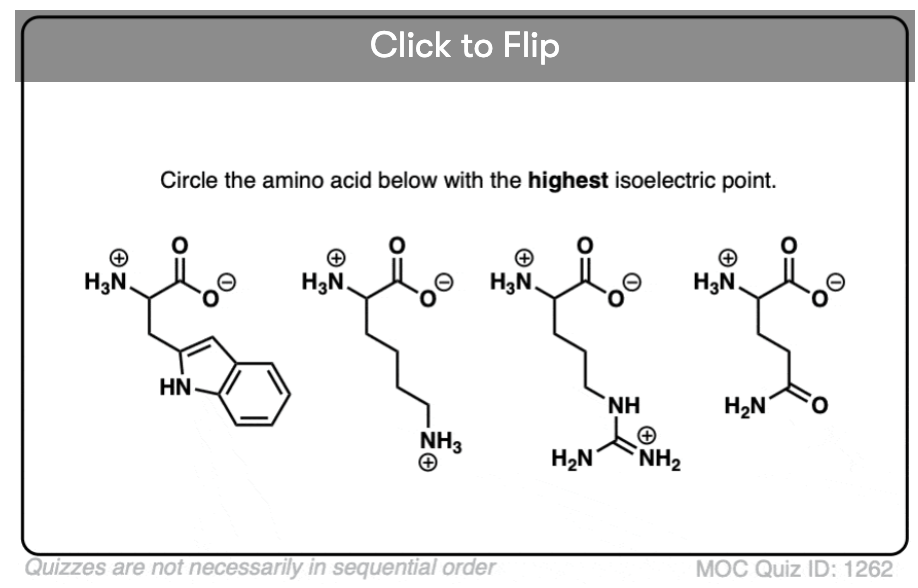
5. Basic Side Chains
There are also amino acids with basic side chains, such as lysine, arginine and histidine.
These amino acids have functional groups that will affect the isoelectric point in the opposite direction.
For lysine, the different forms of the amino acid would look like this:
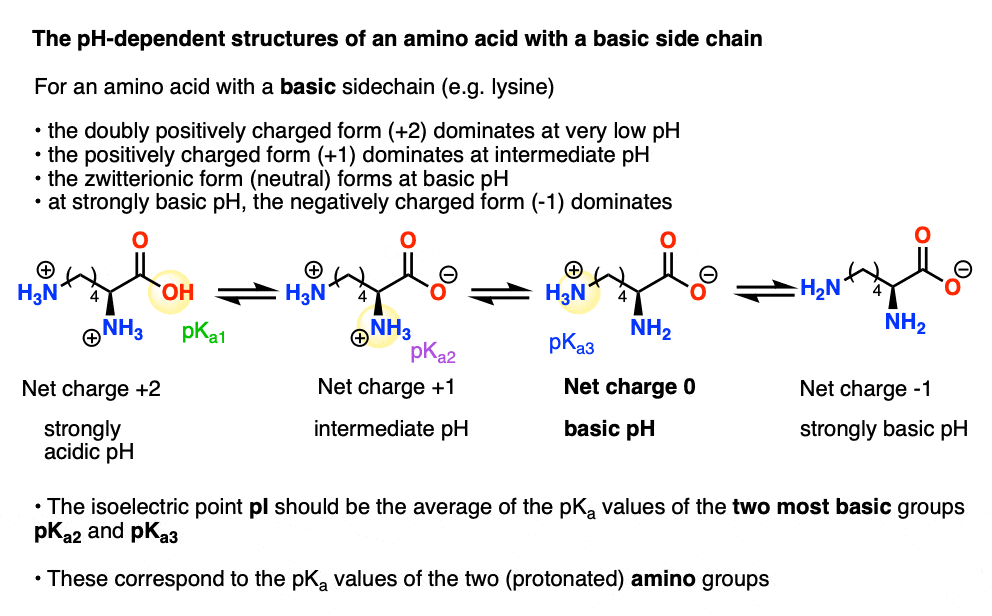
- at extremely low pH, the carboxylic acid and both amine groups are protonated to give a species with a net charge of +2
- At intermediate pH, the carboxylic acid is deprotonated to give a species with a net charge of +1
- At basic pH, the most acidic ammonium will be deprotonated to give the neutral species with a (net) charge of 0
- At strongly basic pH, both ammoniums will be deprotonated to give a species with a net charge of -1.
The isoelectric point will be the pH at which the molecule bears a net charge of zero.
The neutral species is formed through deprotonation of the most acidic ammonium (pKa2 = 8.95) and destroyed through deprotonation of the least acidic ammonium (pKa3 = 10.53).
So averaging these two pKa values should give us the isoelectric point, pI.
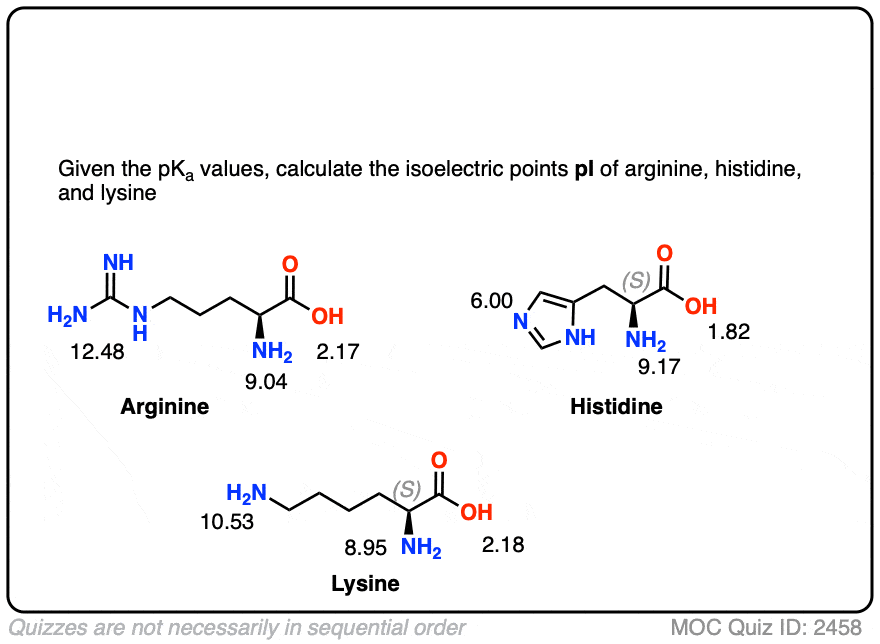
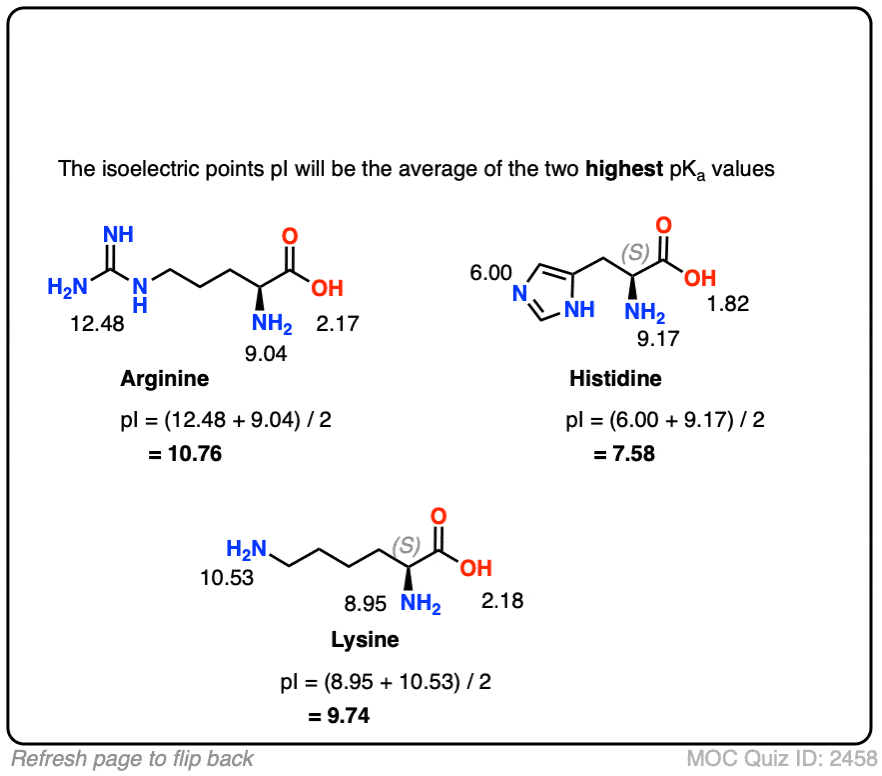
See if you can calculate the pI of these basic amino acids.
 Click to Flip
Click to Flip
6. Summary
There is more to isoelectric point than just the calculation of pI values for individual amino acids! The same concepts also apply to peptides and proteins, each of which will have a pI value that is influenced by the characteristics of its side chains.
These differences form the basis of electrophoresis, an effective technique for the separation of these molecules through adjustment of pH and application of an electric field.
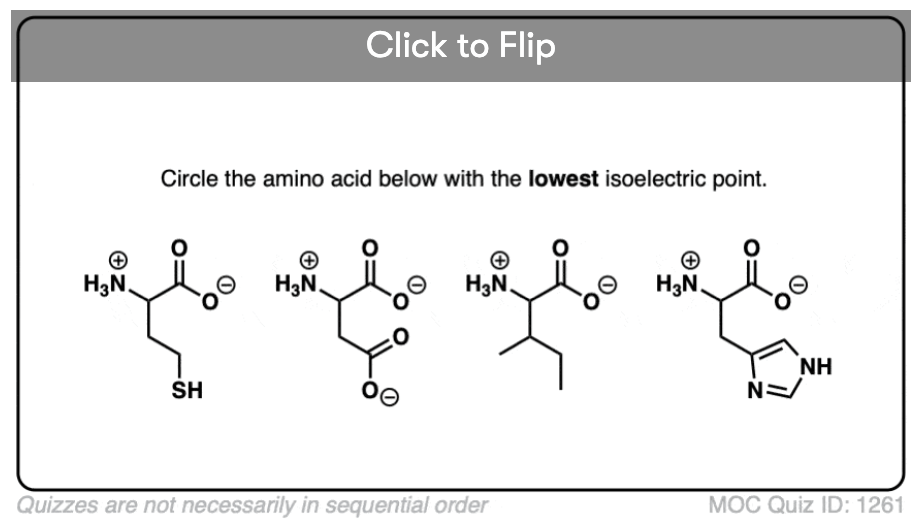
Quiz Yourself!

Become a MOC member to see the clickable quiz with answers on the back.
Become a MOC member to see the clickable quiz with answers on the back.
Become a MOC member to see the clickable quiz with answers on the back.
Become a MOC member to see the clickable quiz with answers on the back.

Become a MOC member to see the clickable quiz with answers on the back.
Notes
Related Articles
Note 1. More detailed calculations of titration curves can be obtained with the help of software such as Hyperquad – see here.
Note 2. The calculation ends up being so simple because the second term of the Henderson Hasselbalch equation ends up cancelling out:
(Advanced) References and Further Reading
00 General Chemistry Review
01 Bonding, Structure, and Resonance
- How Do We Know Methane (CH4) Is Tetrahedral?
- Hybrid Orbitals and Hybridization
- How To Determine Hybridization: A Shortcut
- Orbital Hybridization And Bond Strengths
- Sigma bonds come in six varieties: Pi bonds come in one
- A Key Skill: How to Calculate Formal Charge
- The Four Intermolecular Forces and How They Affect Boiling Points
- 3 Trends That Affect Boiling Points
- How To Use Electronegativity To Determine Electron Density (and why NOT to trust formal charge)
- Introduction to Resonance
- How To Use Curved Arrows To Interchange Resonance Forms
- Evaluating Resonance Forms (1) - The Rule of Least Charges
- How To Find The Best Resonance Structure By Applying Electronegativity
- Evaluating Resonance Structures With Negative Charges
- Evaluating Resonance Structures With Positive Charge
- Exploring Resonance: Pi-Donation
- Exploring Resonance: Pi-acceptors
- In Summary: Evaluating Resonance Structures
- Drawing Resonance Structures: 3 Common Mistakes To Avoid
- How to apply electronegativity and resonance to understand reactivity
- Bond Hybridization Practice
- Structure and Bonding Practice Quizzes
- Resonance Structures Practice
02 Acid Base Reactions
- Introduction to Acid-Base Reactions
- Acid Base Reactions In Organic Chemistry
- The Stronger The Acid, The Weaker The Conjugate Base
- Walkthrough of Acid-Base Reactions (3) - Acidity Trends
- Five Key Factors That Influence Acidity
- Acid-Base Reactions: Introducing Ka and pKa
- How to Use a pKa Table
- The pKa Table Is Your Friend
- A Handy Rule of Thumb for Acid-Base Reactions
- Acid Base Reactions Are Fast
- pKa Values Span 60 Orders Of Magnitude
- How Protonation and Deprotonation Affect Reactivity
- Acid Base Practice Problems
03 Alkanes and Nomenclature
- Meet the (Most Important) Functional Groups
- Condensed Formulas: Deciphering What the Brackets Mean
- Hidden Hydrogens, Hidden Lone Pairs, Hidden Counterions
- Don't Be Futyl, Learn The Butyls
- Primary, Secondary, Tertiary, Quaternary In Organic Chemistry
- Branching, and Its Affect On Melting and Boiling Points
- The Many, Many Ways of Drawing Butane
- Wedge And Dash Convention For Tetrahedral Carbon
- Common Mistakes in Organic Chemistry: Pentavalent Carbon
- Table of Functional Group Priorities for Nomenclature
- Summary Sheet - Alkane Nomenclature
- Organic Chemistry IUPAC Nomenclature Demystified With A Simple Puzzle Piece Approach
- Boiling Point Quizzes
- Organic Chemistry Nomenclature Quizzes
04 Conformations and Cycloalkanes
- Staggered vs Eclipsed Conformations of Ethane
- Conformational Isomers of Propane
- Newman Projection of Butane (and Gauche Conformation)
- Introduction to Cycloalkanes
- Geometric Isomers In Small Rings: Cis And Trans Cycloalkanes
- Calculation of Ring Strain In Cycloalkanes
- Cycloalkanes - Ring Strain In Cyclopropane And Cyclobutane
- Cyclohexane Conformations
- Cyclohexane Chair Conformation: An Aerial Tour
- How To Draw The Cyclohexane Chair Conformation
- The Cyclohexane Chair Flip
- The Cyclohexane Chair Flip - Energy Diagram
- Substituted Cyclohexanes - Axial vs Equatorial
- Ranking The Bulkiness Of Substituents On Cyclohexanes: "A-Values"
- Cyclohexane Chair Conformation Stability: Which One Is Lower Energy?
- Fused Rings - Cis-Decalin and Trans-Decalin
- Naming Bicyclic Compounds - Fused, Bridged, and Spiro
- Bredt's Rule (And Summary of Cycloalkanes)
- Newman Projection Practice
- Cycloalkanes Practice Problems
05 A Primer On Organic Reactions
- The Most Important Question To Ask When Learning a New Reaction
- Curved Arrows (for reactions)
- Nucleophiles and Electrophiles
- The Three Classes of Nucleophiles
- Nucleophilicity vs. Basicity
- What Makes A Good Nucleophile?
- What Makes A Good Leaving Group?
- 3 Factors That Stabilize Carbocations
- Equilibrium and Energy Relationships
- 7 Factors that stabilize negative charge in organic chemistry
- 7 Factors That Stabilize Positive Charge in Organic Chemistry
- What's a Transition State?
- Hammond's Postulate
- Learning Organic Chemistry Reactions: A Checklist (PDF)
- Introduction to Oxidative Cleavage Reactions
06 Free Radical Reactions
- Bond Dissociation Energies = Homolytic Cleavage
- Free Radical Reactions
- 3 Factors That Stabilize Free Radicals
- What Factors Destabilize Free Radicals?
- Bond Strengths And Radical Stability
- Free Radical Initiation: Why Is "Light" Or "Heat" Required?
- Initiation, Propagation, Termination
- Monochlorination Products Of Propane, Pentane, And Other Alkanes
- Selectivity In Free Radical Reactions
- Selectivity in Free Radical Reactions: Bromination vs. Chlorination
- Halogenation At Tiffany's
- Allylic Bromination
- Bonus Topic: Allylic Rearrangements
- In Summary: Free Radicals
- Synthesis (2) - Reactions of Alkanes
- Free Radicals Practice Quizzes
07 Stereochemistry and Chirality
- Types of Isomers: Constitutional Isomers, Stereoisomers, Enantiomers, and Diastereomers
- How To Draw The Enantiomer Of A Chiral Molecule
- How To Draw A Bond Rotation
- Introduction to Assigning (R) and (S): The Cahn-Ingold-Prelog Rules
- Assigning Cahn-Ingold-Prelog (CIP) Priorities (2) - The Method of Dots
- Enantiomers vs Diastereomers vs The Same? Two Methods For Solving Problems
- Assigning R/S To Newman Projections (And Converting Newman To Line Diagrams)
- How To Determine R and S Configurations On A Fischer Projection
- The Meso Trap
- Optical Rotation, Optical Activity, and Specific Rotation
- Optical Purity and Enantiomeric Excess
- What's a Racemic Mixture?
- Chiral Allenes And Chiral Axes
- Stereochemistry Practice Problems and Quizzes
08 Substitution Reactions
- Nucleophilic Substitution Reactions - Introduction
- Two Types of Nucleophilic Substitution Reactions
- The SN2 Mechanism
- Why the SN2 Reaction Is Powerful
- The SN1 Mechanism
- The Conjugate Acid Is A Better Leaving Group
- Comparing the SN1 and SN2 Reactions
- Polar Protic? Polar Aprotic? Nonpolar? All About Solvents
- Steric Hindrance is Like a Fat Goalie
- Common Blind Spot: Intramolecular Reactions
- Substitution Practice - SN1
- Substitution Practice - SN2
09 Elimination Reactions
- Elimination Reactions (1): Introduction And The Key Pattern
- Elimination Reactions (2): The Zaitsev Rule
- Elimination Reactions Are Favored By Heat
- Two Elimination Reaction Patterns
- The E1 Reaction
- The E2 Mechanism
- E1 vs E2: Comparing the E1 and E2 Reactions
- Antiperiplanar Relationships: The E2 Reaction and Cyclohexane Rings
- Bulky Bases in Elimination Reactions
- Comparing the E1 vs SN1 Reactions
- Elimination (E1) Reactions With Rearrangements
- E1cB - Elimination (Unimolecular) Conjugate Base
- Elimination (E1) Practice Problems And Solutions
- Elimination (E2) Practice Problems and Solutions
10 Rearrangements
11 SN1/SN2/E1/E2 Decision
- Identifying Where Substitution and Elimination Reactions Happen
- Deciding SN1/SN2/E1/E2 (1) - The Substrate
- Deciding SN1/SN2/E1/E2 (2) - The Nucleophile/Base
- SN1 vs E1 and SN2 vs E2 : The Temperature
- Deciding SN1/SN2/E1/E2 - The Solvent
- Wrapup: The Key Factors For Determining SN1/SN2/E1/E2
- Alkyl Halide Reaction Map And Summary
- SN1 SN2 E1 E2 Practice Problems
12 Alkene Reactions
- E and Z Notation For Alkenes (+ Cis/Trans)
- Alkene Stability
- Alkene Addition Reactions: "Regioselectivity" and "Stereoselectivity" (Syn/Anti)
- Stereoselective and Stereospecific Reactions
- Hydrohalogenation of Alkenes and Markovnikov's Rule
- Hydration of Alkenes With Aqueous Acid
- Rearrangements in Alkene Addition Reactions
- Halogenation of Alkenes and Halohydrin Formation
- Oxymercuration Demercuration of Alkenes
- Hydroboration Oxidation of Alkenes
- m-CPBA (meta-chloroperoxybenzoic acid)
- OsO4 (Osmium Tetroxide) for Dihydroxylation of Alkenes
- Palladium on Carbon (Pd/C) for Catalytic Hydrogenation of Alkenes
- Cyclopropanation of Alkenes
- A Fourth Alkene Addition Pattern - Free Radical Addition
- Alkene Reactions: Ozonolysis
- Summary: Three Key Families Of Alkene Reaction Mechanisms
- Synthesis (4) - Alkene Reaction Map, Including Alkyl Halide Reactions
- Alkene Reactions Practice Problems
13 Alkyne Reactions
- Acetylides from Alkynes, And Substitution Reactions of Acetylides
- Partial Reduction of Alkynes With Lindlar's Catalyst
- Partial Reduction of Alkynes With Na/NH3 To Obtain Trans Alkenes
- Alkyne Hydroboration With "R2BH"
- Hydration and Oxymercuration of Alkynes
- Hydrohalogenation of Alkynes
- Alkyne Halogenation: Bromination and Chlorination of Alkynes
- Alkyne Reactions - The "Concerted" Pathway
- Alkenes To Alkynes Via Halogenation And Elimination Reactions
- Alkynes Are A Blank Canvas
- Synthesis (5) - Reactions of Alkynes
- Alkyne Reactions Practice Problems With Answers
14 Alcohols, Epoxides and Ethers
- Alcohols - Nomenclature and Properties
- Alcohols Can Act As Acids Or Bases (And Why It Matters)
- Alcohols - Acidity and Basicity
- The Williamson Ether Synthesis
- Ethers From Alkenes, Tertiary Alkyl Halides and Alkoxymercuration
- Alcohols To Ethers via Acid Catalysis
- Cleavage Of Ethers With Acid
- Epoxides - The Outlier Of The Ether Family
- Opening of Epoxides With Acid
- Epoxide Ring Opening With Base
- Making Alkyl Halides From Alcohols
- Tosylates And Mesylates
- PBr3 and SOCl2
- Elimination Reactions of Alcohols
- Elimination of Alcohols To Alkenes With POCl3
- Alcohol Oxidation: "Strong" and "Weak" Oxidants
- Demystifying The Mechanisms of Alcohol Oxidations
- Protecting Groups For Alcohols
- Thiols And Thioethers
- Calculating the oxidation state of a carbon
- Oxidation and Reduction in Organic Chemistry
- Oxidation Ladders
- SOCl2 Mechanism For Alcohols To Alkyl Halides: SN2 versus SNi
- Alcohol Reactions Roadmap (PDF)
- Alcohol Reaction Practice Problems
- Epoxide Reaction Quizzes
- Oxidation and Reduction Practice Quizzes
15 Organometallics
- What's An Organometallic?
- Formation of Grignard and Organolithium Reagents
- Organometallics Are Strong Bases
- Reactions of Grignard Reagents
- Protecting Groups In Grignard Reactions
- Synthesis Problems Involving Grignard Reagents
- Grignard Reactions And Synthesis (2)
- Organocuprates (Gilman Reagents): How They're Made
- Gilman Reagents (Organocuprates): What They're Used For
- The Heck, Suzuki, and Olefin Metathesis Reactions (And Why They Don't Belong In Most Introductory Organic Chemistry Courses)
- Reaction Map: Reactions of Organometallics
- Grignard Practice Problems
16 Spectroscopy
- Degrees of Unsaturation (or IHD, Index of Hydrogen Deficiency)
- Conjugation And Color (+ How Bleach Works)
- Introduction To UV-Vis Spectroscopy
- UV-Vis Spectroscopy: Absorbance of Carbonyls
- UV-Vis Spectroscopy: Practice Questions
- Bond Vibrations, Infrared Spectroscopy, and the "Ball and Spring" Model
- Infrared Spectroscopy: A Quick Primer On Interpreting Spectra
- IR Spectroscopy: 4 Practice Problems
- 1H NMR: How Many Signals?
- Homotopic, Enantiotopic, Diastereotopic
- Diastereotopic Protons in 1H NMR Spectroscopy: Examples
- 13-C NMR - How Many Signals
- Liquid Gold: Pheromones In Doe Urine
- Natural Product Isolation (1) - Extraction
- Natural Product Isolation (2) - Purification Techniques, An Overview
- Structure Determination Case Study: Deer Tarsal Gland Pheromone
17 Dienes and MO Theory
- What To Expect In Organic Chemistry 2
- Are these molecules conjugated?
- Conjugation And Resonance In Organic Chemistry
- Bonding And Antibonding Pi Orbitals
- Molecular Orbitals of The Allyl Cation, Allyl Radical, and Allyl Anion
- Pi Molecular Orbitals of Butadiene
- Reactions of Dienes: 1,2 and 1,4 Addition
- Thermodynamic and Kinetic Products
- More On 1,2 and 1,4 Additions To Dienes
- s-cis and s-trans
- The Diels-Alder Reaction
- Cyclic Dienes and Dienophiles in the Diels-Alder Reaction
- Stereochemistry of the Diels-Alder Reaction
- Exo vs Endo Products In The Diels Alder: How To Tell Them Apart
- HOMO and LUMO In the Diels Alder Reaction
- Why Are Endo vs Exo Products Favored in the Diels-Alder Reaction?
- Diels-Alder Reaction: Kinetic and Thermodynamic Control
- The Retro Diels-Alder Reaction
- The Intramolecular Diels Alder Reaction
- Regiochemistry In The Diels-Alder Reaction
- The Cope and Claisen Rearrangements
- Electrocyclic Reactions
- Electrocyclic Ring Opening And Closure (2) - Six (or Eight) Pi Electrons
- Diels Alder Practice Problems
- Molecular Orbital Theory Practice
18 Aromaticity
- Introduction To Aromaticity
- Rules For Aromaticity
- Huckel's Rule: What Does 4n+2 Mean?
- Aromatic, Non-Aromatic, or Antiaromatic? Some Practice Problems
- Antiaromatic Compounds and Antiaromaticity
- The Pi Molecular Orbitals of Benzene
- The Pi Molecular Orbitals of Cyclobutadiene
- Frost Circles
- Aromaticity Practice Quizzes
19 Reactions of Aromatic Molecules
- Electrophilic Aromatic Substitution: Introduction
- Activating and Deactivating Groups In Electrophilic Aromatic Substitution
- Electrophilic Aromatic Substitution - The Mechanism
- Ortho-, Para- and Meta- Directors in Electrophilic Aromatic Substitution
- Understanding Ortho, Para, and Meta Directors
- Why are halogens ortho- para- directors?
- Disubstituted Benzenes: The Strongest Electron-Donor "Wins"
- Electrophilic Aromatic Substitutions (1) - Halogenation of Benzene
- Electrophilic Aromatic Substitutions (2) - Nitration and Sulfonation
- EAS Reactions (3) - Friedel-Crafts Acylation and Friedel-Crafts Alkylation
- Intramolecular Friedel-Crafts Reactions
- Nucleophilic Aromatic Substitution (NAS)
- Nucleophilic Aromatic Substitution (2) - The Benzyne Mechanism
- Reactions on the "Benzylic" Carbon: Bromination And Oxidation
- The Wolff-Kishner, Clemmensen, And Other Carbonyl Reductions
- More Reactions on the Aromatic Sidechain: Reduction of Nitro Groups and the Baeyer Villiger
- Aromatic Synthesis (1) - "Order Of Operations"
- Synthesis of Benzene Derivatives (2) - Polarity Reversal
- Aromatic Synthesis (3) - Sulfonyl Blocking Groups
- Birch Reduction
- Synthesis (7): Reaction Map of Benzene and Related Aromatic Compounds
- Aromatic Reactions and Synthesis Practice
- Electrophilic Aromatic Substitution Practice Problems
20 Aldehydes and Ketones
- What's The Alpha Carbon In Carbonyl Compounds?
- Nucleophilic Addition To Carbonyls
- Aldehydes and Ketones: 14 Reactions With The Same Mechanism
- Sodium Borohydride (NaBH4) Reduction of Aldehydes and Ketones
- Grignard Reagents For Addition To Aldehydes and Ketones
- Wittig Reaction
- Hydrates, Hemiacetals, and Acetals
- Imines - Properties, Formation, Reactions, and Mechanisms
- All About Enamines
- Breaking Down Carbonyl Reaction Mechanisms: Reactions of Anionic Nucleophiles (Part 2)
- Aldehydes Ketones Reaction Practice
21 Carboxylic Acid Derivatives
- Nucleophilic Acyl Substitution (With Negatively Charged Nucleophiles)
- Addition-Elimination Mechanisms With Neutral Nucleophiles (Including Acid Catalysis)
- Basic Hydrolysis of Esters - Saponification
- Transesterification
- Proton Transfer
- Fischer Esterification - Carboxylic Acid to Ester Under Acidic Conditions
- Lithium Aluminum Hydride (LiAlH4) For Reduction of Carboxylic Acid Derivatives
- LiAlH[Ot-Bu]3 For The Reduction of Acid Halides To Aldehydes
- Di-isobutyl Aluminum Hydride (DIBAL) For The Partial Reduction of Esters and Nitriles
- Amide Hydrolysis
- Thionyl Chloride (SOCl2) And Conversion of Carboxylic Acids to Acid Halides
- Diazomethane (CH2N2)
- Carbonyl Chemistry: Learn Six Mechanisms For the Price Of One
- Making Music With Mechanisms (PADPED)
- Carboxylic Acid Derivatives Practice Questions
22 Enols and Enolates
- Keto-Enol Tautomerism
- Enolates - Formation, Stability, and Simple Reactions
- Kinetic Versus Thermodynamic Enolates
- Aldol Addition and Condensation Reactions
- Reactions of Enols - Acid-Catalyzed Aldol, Halogenation, and Mannich Reactions
- Claisen Condensation and Dieckmann Condensation
- Decarboxylation
- The Malonic Ester and Acetoacetic Ester Synthesis
- The Michael Addition Reaction and Conjugate Addition
- The Robinson Annulation
- Haloform Reaction
- The Hell–Volhard–Zelinsky Reaction
- Enols and Enolates Practice Quizzes
23 Amines
- The Amide Functional Group: Properties, Synthesis, and Nomenclature
- Basicity of Amines And pKaH
- 5 Key Basicity Trends of Amines
- The Mesomeric Effect And Aromatic Amines
- Nucleophilicity of Amines
- Alkylation of Amines (Sucks!)
- Reductive Amination
- The Gabriel Synthesis
- Some Reactions of Azides
- The Hofmann Elimination
- The Hofmann and Curtius Rearrangements
- The Cope Elimination
- Protecting Groups for Amines - Carbamates
- The Strecker Synthesis of Amino Acids
- Introduction to Peptide Synthesis
- Reactions of Diazonium Salts: Sandmeyer and Related Reactions
- Amine Practice Questions
24 Carbohydrates
- D and L Notation For Sugars
- Pyranoses and Furanoses: Ring-Chain Tautomerism In Sugars
- What is Mutarotation?
- Reducing Sugars
- The Big Damn Post Of Carbohydrate-Related Chemistry Definitions
- The Haworth Projection
- Converting a Fischer Projection To A Haworth (And Vice Versa)
- Reactions of Sugars: Glycosylation and Protection
- The Ruff Degradation and Kiliani-Fischer Synthesis
- Isoelectric Points of Amino Acids (and How To Calculate Them)
- Carbohydrates Practice
- Amino Acid Quizzes
25 Fun and Miscellaneous
- A Gallery of Some Interesting Molecules From Nature
- Screw Organic Chemistry, I'm Just Going To Write About Cats
- On Cats, Part 1: Conformations and Configurations
- On Cats, Part 2: Cat Line Diagrams
- On Cats, Part 4: Enantiocats
- On Cats, Part 6: Stereocenters
- Organic Chemistry Is Shit
- The Organic Chemistry Behind "The Pill"
- Maybe they should call them, "Formal Wins" ?
- Why Do Organic Chemists Use Kilocalories?
- The Principle of Least Effort
- Organic Chemistry GIFS - Resonance Forms
- Reproducibility In Organic Chemistry
- What Holds The Nucleus Together?
- How Reactions Are Like Music
- Organic Chemistry and the New MCAT
26 Organic Chemistry Tips and Tricks
- Common Mistakes: Formal Charges Can Mislead
- Partial Charges Give Clues About Electron Flow
- Draw The Ugly Version First
- Organic Chemistry Study Tips: Learn the Trends
- The 8 Types of Arrows In Organic Chemistry, Explained
- Top 10 Skills To Master Before An Organic Chemistry 2 Final
- Common Mistakes with Carbonyls: Carboxylic Acids... Are Acids!
- Planning Organic Synthesis With "Reaction Maps"
- Alkene Addition Pattern #1: The "Carbocation Pathway"
- Alkene Addition Pattern #2: The "Three-Membered Ring" Pathway
- Alkene Addition Pattern #3: The "Concerted" Pathway
- Number Your Carbons!
- The 4 Major Classes of Reactions in Org 1
- How (and why) electrons flow
- Grossman's Rule
- Three Exam Tips
- A 3-Step Method For Thinking Through Synthesis Problems
- Putting It Together
- Putting Diels-Alder Products in Perspective
- The Ups and Downs of Cyclohexanes
- The Most Annoying Exceptions in Org 1 (Part 1)
- The Most Annoying Exceptions in Org 1 (Part 2)
- The Marriage May Be Bad, But the Divorce Still Costs Money
- 9 Nomenclature Conventions To Know
- Nucleophile attacks Electrophile
27 Case Studies of Successful O-Chem Students
- Success Stories: How Corina Got The The "Hard" Professor - And Got An A+ Anyway
- How Helena Aced Organic Chemistry
- From a "Drop" To B+ in Org 2 – How A Hard Working Student Turned It Around
- How Serge Aced Organic Chemistry
- Success Stories: How Zach Aced Organic Chemistry 1
- Success Stories: How Kari Went From C– to B+
- How Esther Bounced Back From a "C" To Get A's In Organic Chemistry 1 And 2
- How Tyrell Got The Highest Grade In Her Organic Chemistry Course
- This Is Why Students Use Flashcards
- Success Stories: How Stu Aced Organic Chemistry
- How John Pulled Up His Organic Chemistry Exam Grades
- Success Stories: How Nathan Aced Organic Chemistry (Without It Taking Over His Life)
- How Chris Aced Org 1 and Org 2
- Interview: How Jay Got an A+ In Organic Chemistry
- How to Do Well in Organic Chemistry: One Student's Advice
- "America's Top TA" Shares His Secrets For Teaching O-Chem
- "Organic Chemistry Is Like..." - A Few Metaphors
- How To Do Well In Organic Chemistry: Advice From A Tutor
- Guest post: "I went from being afraid of tests to actually looking forward to them".
hello. may we look at this sentence at this sentence “For amino acids with basic sidechains, the pI can be calculated by averaging the pKa values of the least acidic groups”. Is it making sence?
kindly regards.
If you’re given an amino acid with a basic sidechain and its three pka values: pka1, pka2, and pka3, then to determine the pI of this molecule, take the average of pka2 and pka3.
Thanks a million ! Great job.
Well summarised and easy to understand. Thankyu
Great explanations! Shouldn’t the pI equation that is in the dotted border in section 3. be pI= (pKa1+pKa2)/2? The formula in the dashed border is missing a denominator of 2.
Oh snap – you are correct, thank you very much for spotting this. Fixed!
Notes are well explained