Home / Optical Rotation, Optical Activity, and Specific Rotation
Stereochemistry and Chirality
Optical Rotation, Optical Activity, and Specific Rotation
Last updated: July 3rd, 2025 |
Optical Rotation, Optical Activity, and Specific Rotation
If you’ve been learning about stereochemistry, enantiomers, and diastereomers, the following might sound familiar:
- Diastereomers have different physical properties (i.e. boiling points, melting points, solubilities)
- Enantiomers have identical physical properties* , with one exception: enantiomers rotate plane-polarized light in equal and opposite directions, which is why they are sometimes called “optical isomers”.
*(assuming an achiral environment)
[If you’re unclear on the difference between enantiomers and diastereomers, I’d suggest going back to this post]
What does that term “optical rotation” mean? Or, for that matter, “optical activity”? You might also have heard of “specific rotation”. What’s that? We’ll cover all of these concepts below.
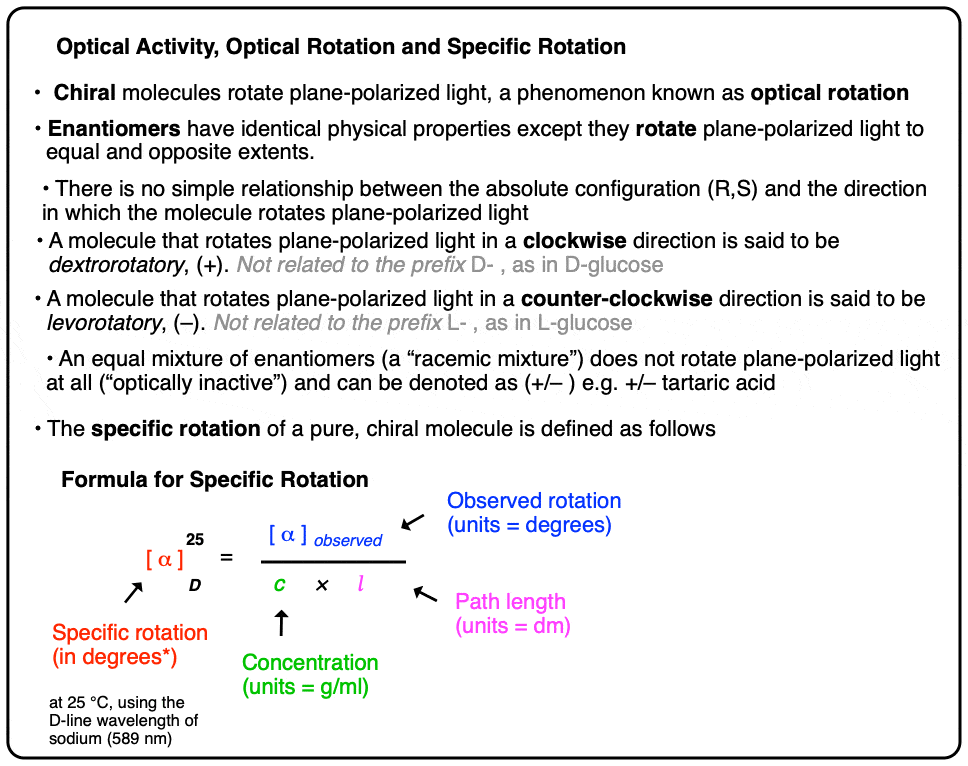
Table of Contents
- Louis Pasteur’s Discovery of “Left-Handed” and “Right-Handed” Tartaric Acid Crystals
- The Three Stereoisomers Of Tartaric Acid, And How They Are Related
- Do Molecules With An (R) Configuration always Rotate Plane-Polarized Light To The Right? (Hint: No)
- Untangling The Differences Between R and S, D- and L- , d- and l-, and (+)- and (–)-
- Polarimetry: The Measurement of Optical Rotation
- Specific Rotation: A Common Standard For Comparing Optical Rotation
- Specific Rotation: A Sample Problem
- Conclusion: Optical Rotation And Specific Rotation
- Notes
- Quiz Yourself!
- (Advanced) References and Further Reading
This post was co-authored with Matt Pierce of Organic Chemistry Solutions. Ask Matt about scheduling an online tutoring session here.
1. Louis Pasteur’s Discovery of “Left-Handed” and “Right-Handed” Tartaric Acid Crystals
Louis Pasteur is more than just the man whose name was lent to the process of “pasteurization”. He is also the father of organic stereochemistry . In 1848, Pasteur published a study on the recrystallization of various salts of tartaric acid, or “tartrates”, which are found naturally in wine (aka “wine diamonds”).

Of particular interest to Pasteur were the crystalline forms “racemic acid” (from the Latin racemus for “a bunch of grapes”), which at that time was thought to be an isomer of tartaric acid.
At the time, it was known that racemic acid did not turn the plane of polarized light, whereas “tartar”, the most common salt of tartaric acid, rotated plane-polarized light to the right [“dextrorotatory”, or (+) ]
Upon close inspection, Pasteur noticed that the potassium sodium salt of “racemic acid” crystallized in two separate crystal forms which were mirror images of each other. According to rules of crystal morphology, one type was “right handed”, and the other was “left handed” . [Maybe you’ve heard of “left-handed” and “right handed” screws? The process of naming left and right-handed crystals is similar. ]

This was a strange result, since there was no reason to think that crystals that did not themselves rotate plane-polarized light should have any chirality. Pasteur carefully arranged the crystals and discovered that one half of them were right handed and the other half were left handed. Taken into aqueous solution, the right-handed crystals were dextrorotatory (exactly like crystals of “tartar”, from wine) and the left-handed crystals were levorotatory, to precisely the same degree.
From this Pasteur postulated that the two molecules were mirror images of each other – even though it would be years before the absolute structure of tartaric acid was known, and 25 years before Van’t Hoff proposed the tetrahedral shape of carbon as a means of explaining the existence of optical isomers. [Note 2]
2. The Structure of The Three Stereoisomers Of Tartaric Acid
We now know that what Pasteur called “racemic acid” was not a single compound, but in fact a mixture of two enantiomers of tartrate. Upon crystallization, the [S,S] and [R,R] enantiomers gave different crystals which Pasteur separated mechanically, i.e. by hand. [Note: in the figure below, we show “tartaric acids”; Pasteur did his work on the salts of the conjugate bases, which we call “tartrates”]
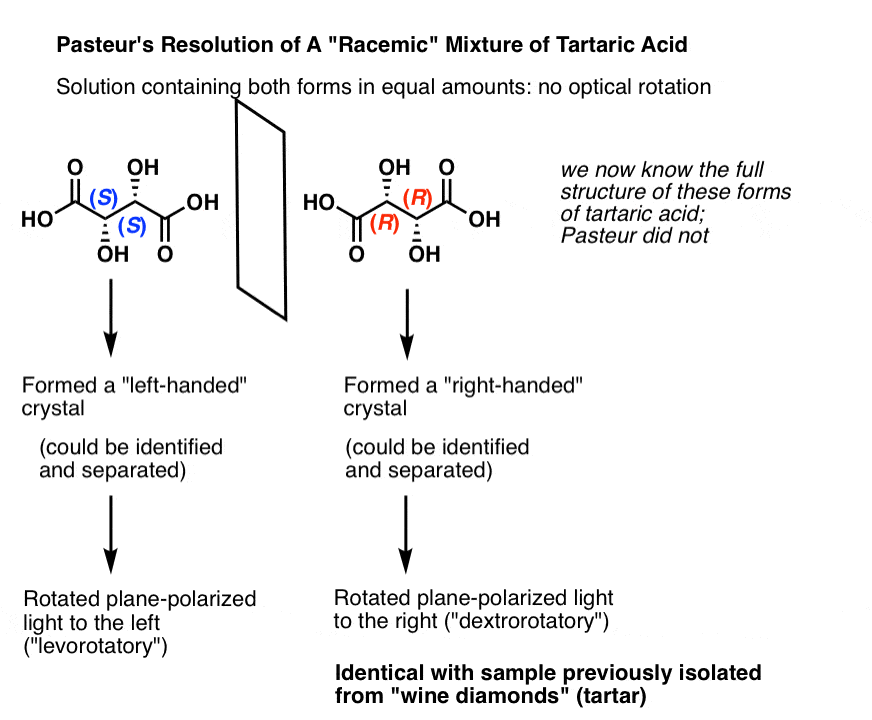
In isolation (S,S) tartaric acid rotates plane-polarized light to the left, and (R,R) tartaric acid rotates plane-polarized light to the right. Naturally occurring wine diamonds are (R,R) and thus dextrorotatory.
Thus these are called “optical isomers” in that they differ solely in the direction of their optical rotation.
By the way, Pasteur also studied a third form of tartaric acid that does not rotate plane-polarized light at all. This form was called “meso” (Greek for middle, since the light was rotated neither to the left nor the right). The configuration of the two chiral centers were subsequently determined to be (R,S).
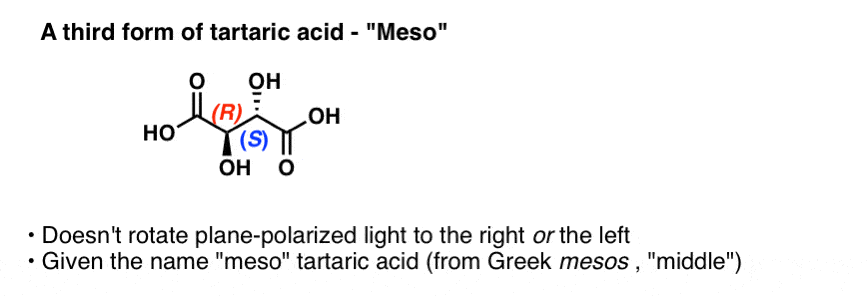
If you’ve covered chirality at all, this term “meso” might be familiar to you. Despite having two chiral enters, “meso” tartaric acid has an internal plane of symmetry and is therefore not a chiral molecule. The name “meso” has come to denote a whole class of compounds that bear chiral centers but are not themselves chiral.

3. Do Molecules With An (R) Configuration always Rotate Plane-Polarized Light To The Right? (Hint: No)
Sometimes you might see a molecule that rotates plane-polarized light to the right (dextrorotatory) described as (+) and a molecule that rotates plane-polarized light to the left (levorotatory) as (–).
Hence, we can have (+)-tartaric acid and (–)-tartaric acid, (+)-glucose and (–)-glucose, and (+)-morphine and (–)-morphine – all pairs of enantiomers.
We also noted that (+)-tartaric acid is (R,R) and (–) tartaric acid is (S,S).
All this begs a question. What is the relationship between the direction of optical rotation and the structure of a molecule? Are molecules with an (R) configuration always dextrorotatory, and molecules with an (S) configuration always levorotatory?
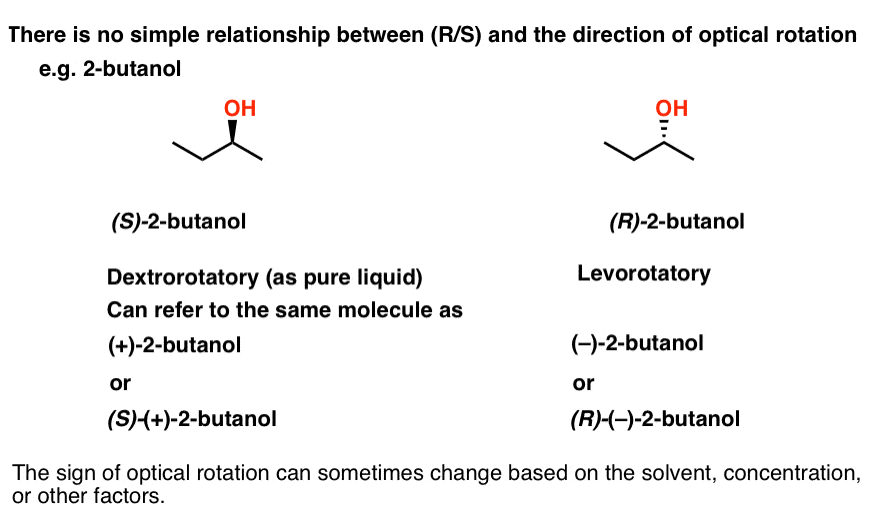
No! There is no simple way to predict the direction of rotation based on the structure. If you want to know what direction a molecule rotates polarized light, you just have to measure it.
For example, (S)-2-butanol is dextrorotatory (+)as a pure liquid, while (R)-2-butanol is levorotatory (–). If we wish, we could also describe (S)-2-butanol as (+)-2-butanol, or even (S)-(+)-2-butanol if you prefer.
4. Untangling The Differences Between R and S, D- and L- , d- and l-, and (+)- and (–)-
This of the problems with discussing a relatively old field like organic stereochemistry is that there are many layers of terminology, some obsolete, that must be peeled away.
The Cahn-Ingold-Prelog system [the origin of naming chiral centers (R) and (S) ] is a relatively new development, dating back to 1951.
(R) and (S) describe the absolute stereochemistry of chiral centers, which you can use to draw the molecule if you know the connectivity of a molecule and understand how to apply the system.
The (R,S) system only became possible once the absolute configuration of molecules could be confirmed, which itself only became possible with the development of X-ray crystallography. [Specifically, Bijouvet in 1951 determined the absolute structure of sodium rubidibum (+)-tartrate using the “heavy atom” method.]
Before the (R,S) system, we had the D, L- system, which were based on Emil Fischer’s guess of the absolute structure of (+)-glyceraldehyde, and then applied to other molecules through chemical analogy. [Note 1].
For example, the levorotatory (–) form of tartaric acid (S, S) is also sometimes described as D-tartaric acid for reasons we won’t go in to here, and conversely, the dextrorotary form (R, R) is described as L-tartaric acid. You see the terms D– and L– also used for amino acids; the essential amino acids are all L.
To add to the confusion, sometimes lowercase “d” and “l” are used to abbreviate “dextrorotatory” and “levorotatory” respectively in place of (+) and (–). So we have d-tartaric acid, which is (+), and l-tartaric acid, which is (–). If we have a mixture of the two (a racemic mixture) you might see this referred to as dl-tartaric acid. Note that IUPAC has designated these terms as obsolete – use (+)/(–) instead.

5. Polarimetry: The Measurement of Optical Rotation
Let’s briefly delve into what got us into this situation in the first place: the measurement of optical rotation. It has been known since at least the 1810s that certain crystals (e.g. quartz) had chiral forms that rotated plane-polarized light in equal and opposite directions. Furthermore, solutions of glucose and turpentine were measured using this technique and shown to be optically active.
Although the equipment has changed, the technique of polarimetry is no different than it was in Pasteur and Biot’s day. The first step is to pass light through a polarizer, which only allows light with waves aligned in one direction to pass. This polarized light is then transmitted through the material to be studied, in our case a cell containing a solution of the molecule.

At the other end, a second polarizer is rotated a given angle θ until this light is transmitted through the slit. Obviously if the solution is not optically active at all, this angle will be zero.
Here is a diagram of a modern polarimeter. Image source: wikipedia
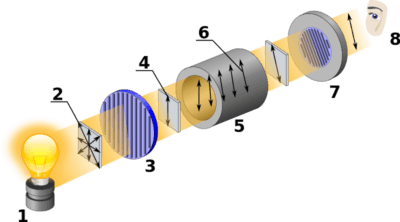
The technical details of how early scientists obtained polarized light are pretty fascinating. More detail here.
6. Specific Rotation: A Common Standard For Comparing Optical Rotation
Now comes the final piece of the puzzle: standardization. It would be useful to have a common standard for optical rotation that allowed us to compare samples collected under slightly different concentrations and path lengths, a little bit like how earned run average (ERA) allows for comparison of performance between pitchers, or goals against average (GAA) for goalies, or batting average, or quarterback passer rating… you can pick your own sports metaphor.
The term that has been developed for this is specific rotation.
The specific rotation of a molecule is the rotation in degrees observed upon passing polarized light through a path length of 1 decimetre (dm) at a concentration of 1 g/mL.
To convert an observed rotation to specific rotation, divide the observed rotation by the concentration in g/mL and the path length in decimeters (dm).
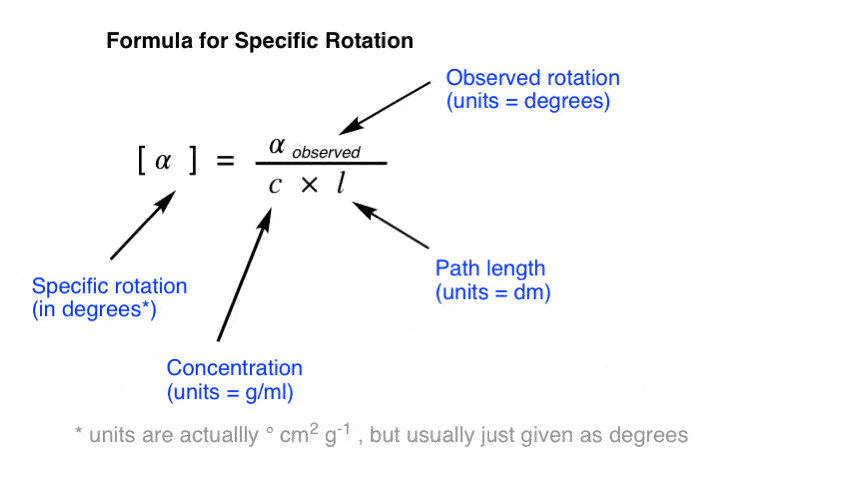
NOTE: As commenter Dr. Fred points out, in most cases dissolving a whole gram of material into a millilitre of solvent is impractical! In laboratory settings, concentration is measured in g / 100 mL and a correction factor of 100 is applied to the numerator. Values of c from the literature should be assumed to be in g / 100 mL.
For reporting purposes, the specific rotation is usually accompanied by the wavelength (often the D-line of sodium, 589 nm) and the temperature. Here’s an example for D-(+)-glucose.

7. Calculation of Specific Rotation: A Sample Problem
Most problems involving specific rotation will ultimately just require a bit of high school algebra. “Plug and chug,” so to speak. Here’s an example:
A sample containing a single enantiomer of fluoxetine (Prozac) is placed in a polarimeter. The observed rotation is 9.06° clockwise. The sample was made by dissolving 1.24 g of fluoxetine in a solution with a total volume of 2.62 mL. The light source was a sodium D line and the temperature was 25° C. The length of the sample tube was 1.25 dm.
You can solve this problem with the following steps.
[α] = [+ 9.06° ] / [(1.24 g/ 2.62 mL)(1.25 dm)]
[α] = +15.3°
Note that we usually just report this number in degrees, although the actual units are degrees cm2 g-1
8. Conclusion: Optical Rotation And Specific Rotation
This post briefly covered some of the main details of optical rotation and specific rotation. In the next post, we’ll explore the relationship between specific rotation and a concept called “enantiomeric excess”.
Questions or comments about this post? Leave one below!
Thanks again to Matt for helping with this post. Hire Matt as your tutor!
Notes
Related Articles
- Optical Purity and Enantiomeric Excess
- What’s a Racemic Mixture?
- Enantiomers vs Diastereomers vs The Same? Two Methods For Solving Problems
- Types of Isomers: Constitutional Isomers, Stereoisomers, Enantiomers, and Diastereomers
- Geometric Isomers In Small Rings: Cis And Trans Cycloalkanes
- Assigning R/S To Newman Projections (And Converting Newman To Line Diagrams)
- How To Determine R and S Configurations On A Fischer Projection
- Stereochemistry Practice Problems and Quizzes (MOC Membership)
Note 1. Thank whatever god you wish to pray to that Fischer guessed correctly, because the old chemical literature would be a bloody nightmare to navigate if he had guessed wrong.
Note 2. Material in this paragraph was adapted from this excellent historical article by crystallographer Howard Flack – highly recommended. In particular, I love Pasteur’s account of demonstrating the resolution of racemic acid to his mentor, Biot.
From John Herschel’s 1822 publication (online here) – a student of organic chemistry might find the following description familiar…
Quiz Yourself!
Become a MOC member to see the clickable quiz with answers on the back.
Become a MOC member to see the clickable quiz with answers on the back.
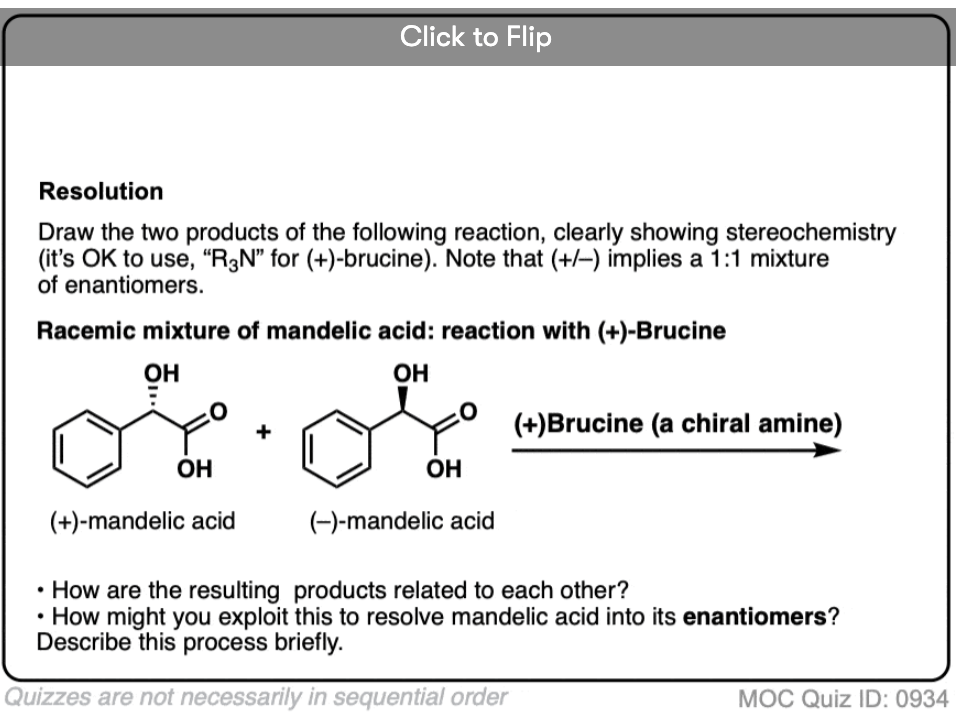
Become a MOC member to see the clickable quiz with answers on the back.
(Advanced) References and Further Reading
- Vogel’s Textbook of Practical Organic Chemistry, 5th Edition, rev. by Brian S. Furniss et. al. 1989. John Wiley & Sons, NY, 1991. Page 248.
- The resolution of racemic acid: A classic stereochemical experiment for the undergraduate laboratory
George B. Kauffman and Robin D. Myers
Journal of Chemical Education 1975, 52 (12), 777
DOI: 1021/ed052p777
This paper goes into detail on Pasteur’s life and background and also shows how Pasteur’s experiment can be repeated by undergraduates! - The discovery of biological enantioselectivity: Louis Pasteur and the fermentation of tartaric acid, 1857—A review and analysis 150 yr later
Joseph Gal
Chirality 2008, 20 (1), 5-19
DOI: 1002/chir.20494
Another historical review discussion Pasteur’s life and his work on the fundamentals of chirality in organic chemistry. - A model for optical rotation
L. L. Jones and Henry Eyring
Journal of Chemical Education 1961, 38 (12), 601
DOI: 10.1021/ed038p601
For those interested in the physics or theoretical underpinnings of the phenomenon of optical rotation, this paper by Prof. Henry Eyring (the same of Eyring equation fame) is a very good read. - Optical rotation
O. M. Evans and H. R. Tietze
Journal of Chemical Education 1964, 41 (12), A973
DOI: 10.1021/ed041pA973.2
Simple procedure for measuring the optical rotation of sucrose. - Optical activity in small molecules, nonenantiomorphous crystals, and nematic liquid crystals
Kenneth O’Loane
Chemical Reviews 1980, 80 (1), 41-61
DOI: 10.1021/cr60323a003
The first of this review is relevant for this topic, and covers Pasteur’s experiment as well as the various forms of chirality in organic small molecules. - IUPAC tentative rules for the nomenclature of organic chemistry. Section E. Fundamental stereochemistry
IUPAC-IUB Comm. on Biochem. Nomenclature
The Journal of Organic Chemistry 1970, 35 (9), 2849-2867
DOI: 1021/jo00834a001
These can be considered as the official IUPAC rules for nomenclature! - Specification of Molecular Chirality
R. S. Cahn, Sir Christopher Ingold, V. Prelog
Angew. Chem. Int. Ed. 1966, 5 (4), 385-415
DOI: 10.1002/anie.196603851
This is not the first paper on the topic by the authors (see Refs. 4 and 5), but it is a major publication and an attempt to consolidate all the information on chirality in a single place. This paper discusses the various types of chirality possible in chemistry (not just at tetrahedral carbons!) and how to assign chirality unambiguously. - Basic Principles of the CIP‐System and Proposals for a Revision
Dr. Vladlmir Prelog and Prof. Dr. Günter Helmchen
Angew. Chem. Int. Ed. 1982, 21 (8), 567-583
DOI: 10.1002/anie.198205671
An update to Ref. #1, which addresses a lot of edge cases that may come up in complex stereochemical assignments. - CHIRALITY IN CHEMISTRY
Vladimir Prelog
Nobel Lecture, 1975
https://www.nobelprize.org/prizes/chemistry/1975/prelog/lecture/
Prelog’s Nobel Lecture. Nobel Lectures are fascinating to read as they give insight into the life of scientists and the path to discovery, which is rarely linear. - “Absolutely” simple stereochemistry
Philip S. Beauchamp
Journal of Chemical Education 1984, 61 (8), 666
DOI: 10.1021/ed061p666
This paper describes a simple method for determining stereochemistry of tetrahedral carbons using the hands, suitable for undergraduate students of organic chemistry. - A simple hand method for Cahn-Ingold-Prelog assignment of R and S configuration to chiral carbons
Martin P. Aalund and James A. Pincock
Journal of Chemical Education 1986, 63 (7), 600
DOI: 10.1021/ed063p600
A follow-up to the previous paper (Ref #4), but sadly it is incomplete! - A Web-Based Stereochemistry Tool to Improve Students’ Ability to Draw Newman Projections and Chair Conformations and Assign R/S Labels
Nimesh Mistry, Ravi Singh, and Jamie Ridley
Journal of Chemical Education 2020, 97 (4), 1157-1161
DOI: 10.1021/acs.jchemed.9b00688
This paper discusses a web-based tool that helps students with visualization of chiral compounds and assignment of stereochemistry as per the Cahn-Ingold-Prelog (CIL) rules. See ref. 34 in the paper for the link.
00 General Chemistry Review
01 Bonding, Structure, and Resonance
- How Do We Know Methane (CH4) Is Tetrahedral?
- Hybrid Orbitals and Hybridization
- How To Determine Hybridization: A Shortcut
- Orbital Hybridization And Bond Strengths
- Sigma bonds come in six varieties: Pi bonds come in one
- A Key Skill: How to Calculate Formal Charge
- The Four Intermolecular Forces and How They Affect Boiling Points
- 3 Trends That Affect Boiling Points
- How To Use Electronegativity To Determine Electron Density (and why NOT to trust formal charge)
- Introduction to Resonance
- How To Use Curved Arrows To Interchange Resonance Forms
- Evaluating Resonance Forms (1) - The Rule of Least Charges
- How To Find The Best Resonance Structure By Applying Electronegativity
- Evaluating Resonance Structures With Negative Charges
- Evaluating Resonance Structures With Positive Charge
- Exploring Resonance: Pi-Donation
- Exploring Resonance: Pi-acceptors
- In Summary: Evaluating Resonance Structures
- Drawing Resonance Structures: 3 Common Mistakes To Avoid
- How to apply electronegativity and resonance to understand reactivity
- Bond Hybridization Practice
- Structure and Bonding Practice Quizzes
- Resonance Structures Practice
02 Acid Base Reactions
- Introduction to Acid-Base Reactions
- Acid Base Reactions In Organic Chemistry
- The Stronger The Acid, The Weaker The Conjugate Base
- Walkthrough of Acid-Base Reactions (3) - Acidity Trends
- Five Key Factors That Influence Acidity
- Acid-Base Reactions: Introducing Ka and pKa
- How to Use a pKa Table
- The pKa Table Is Your Friend
- A Handy Rule of Thumb for Acid-Base Reactions
- Acid Base Reactions Are Fast
- pKa Values Span 60 Orders Of Magnitude
- How Protonation and Deprotonation Affect Reactivity
- Acid Base Practice Problems
03 Alkanes and Nomenclature
- Meet the (Most Important) Functional Groups
- Condensed Formulas: Deciphering What the Brackets Mean
- Hidden Hydrogens, Hidden Lone Pairs, Hidden Counterions
- Don't Be Futyl, Learn The Butyls
- Primary, Secondary, Tertiary, Quaternary In Organic Chemistry
- Branching, and Its Affect On Melting and Boiling Points
- The Many, Many Ways of Drawing Butane
- Wedge And Dash Convention For Tetrahedral Carbon
- Common Mistakes in Organic Chemistry: Pentavalent Carbon
- Table of Functional Group Priorities for Nomenclature
- Summary Sheet - Alkane Nomenclature
- Organic Chemistry IUPAC Nomenclature Demystified With A Simple Puzzle Piece Approach
- Boiling Point Quizzes
- Organic Chemistry Nomenclature Quizzes
04 Conformations and Cycloalkanes
- Staggered vs Eclipsed Conformations of Ethane
- Conformational Isomers of Propane
- Newman Projection of Butane (and Gauche Conformation)
- Introduction to Cycloalkanes
- Geometric Isomers In Small Rings: Cis And Trans Cycloalkanes
- Calculation of Ring Strain In Cycloalkanes
- Cycloalkanes - Ring Strain In Cyclopropane And Cyclobutane
- Cyclohexane Conformations
- Cyclohexane Chair Conformation: An Aerial Tour
- How To Draw The Cyclohexane Chair Conformation
- The Cyclohexane Chair Flip
- The Cyclohexane Chair Flip - Energy Diagram
- Substituted Cyclohexanes - Axial vs Equatorial
- Ranking The Bulkiness Of Substituents On Cyclohexanes: "A-Values"
- Cyclohexane Chair Conformation Stability: Which One Is Lower Energy?
- Fused Rings - Cis-Decalin and Trans-Decalin
- Naming Bicyclic Compounds - Fused, Bridged, and Spiro
- Bredt's Rule (And Summary of Cycloalkanes)
- Newman Projection Practice
- Cycloalkanes Practice Problems
05 A Primer On Organic Reactions
- The Most Important Question To Ask When Learning a New Reaction
- Curved Arrows (for reactions)
- Nucleophiles and Electrophiles
- The Three Classes of Nucleophiles
- Nucleophilicity vs. Basicity
- What Makes A Good Nucleophile?
- What Makes A Good Leaving Group?
- 3 Factors That Stabilize Carbocations
- Equilibrium and Energy Relationships
- 7 Factors that stabilize negative charge in organic chemistry
- 7 Factors That Stabilize Positive Charge in Organic Chemistry
- What's a Transition State?
- Hammond's Postulate
- Learning Organic Chemistry Reactions: A Checklist (PDF)
- Introduction to Oxidative Cleavage Reactions
06 Free Radical Reactions
- Free Radical Reactions
- 3 Factors That Stabilize Free Radicals
- Bond Strengths And Radical Stability
- Free Radical Initiation: Why Is "Light" Or "Heat" Required?
- Initiation, Propagation, Termination
- Monochlorination Products Of Propane, Pentane, And Other Alkanes
- Selectivity In Free Radical Reactions
- Selectivity in Free Radical Reactions: Bromination vs. Chlorination
- Halogenation At Tiffany's
- Allylic Bromination
- Bonus Topic: Allylic Rearrangements
- In Summary: Free Radicals
- Synthesis (2) - Reactions of Alkanes
- Free Radicals Practice Quizzes
07 Stereochemistry and Chirality
- Types of Isomers: Constitutional Isomers, Stereoisomers, Enantiomers, and Diastereomers
- How To Draw The Enantiomer Of A Chiral Molecule
- How To Draw A Bond Rotation
- Introduction to Assigning (R) and (S): The Cahn-Ingold-Prelog Rules
- Assigning Cahn-Ingold-Prelog (CIP) Priorities (2) - The Method of Dots
- Enantiomers vs Diastereomers vs The Same? Two Methods For Solving Problems
- Assigning R/S To Newman Projections (And Converting Newman To Line Diagrams)
- How To Determine R and S Configurations On A Fischer Projection
- The Meso Trap
- Optical Rotation, Optical Activity, and Specific Rotation
- Optical Purity and Enantiomeric Excess
- What's a Racemic Mixture?
- Chiral Allenes And Chiral Axes
- Stereochemistry Practice Problems and Quizzes
08 Substitution Reactions
- Nucleophilic Substitution Reactions - Introduction
- Two Types of Nucleophilic Substitution Reactions
- The SN2 Mechanism
- Why the SN2 Reaction Is Powerful
- The SN1 Mechanism
- The Conjugate Acid Is A Better Leaving Group
- Comparing the SN1 and SN2 Reactions
- Polar Protic? Polar Aprotic? Nonpolar? All About Solvents
- Steric Hindrance is Like a Fat Goalie
- Common Blind Spot: Intramolecular Reactions
- Substitution Practice - SN1
- Substitution Practice - SN2
09 Elimination Reactions
- Elimination Reactions (1): Introduction And The Key Pattern
- Elimination Reactions (2): The Zaitsev Rule
- Elimination Reactions Are Favored By Heat
- Two Elimination Reaction Patterns
- The E1 Reaction
- The E2 Mechanism
- E1 vs E2: Comparing the E1 and E2 Reactions
- Antiperiplanar Relationships: The E2 Reaction and Cyclohexane Rings
- Bulky Bases in Elimination Reactions
- Comparing the E1 vs SN1 Reactions
- Elimination (E1) Reactions With Rearrangements
- E1cB - Elimination (Unimolecular) Conjugate Base
- Elimination (E1) Practice Problems And Solutions
- Elimination (E2) Practice Problems and Solutions
10 Rearrangements
11 SN1/SN2/E1/E2 Decision
- Identifying Where Substitution and Elimination Reactions Happen
- Deciding SN1/SN2/E1/E2 (1) - The Substrate
- Deciding SN1/SN2/E1/E2 (2) - The Nucleophile/Base
- SN1 vs E1 and SN2 vs E2 : The Temperature
- Deciding SN1/SN2/E1/E2 - The Solvent
- Wrapup: The Key Factors For Determining SN1/SN2/E1/E2
- Alkyl Halide Reaction Map And Summary
- SN1 SN2 E1 E2 Practice Problems
12 Alkene Reactions
- E and Z Notation For Alkenes (+ Cis/Trans)
- Alkene Stability
- Alkene Addition Reactions: "Regioselectivity" and "Stereoselectivity" (Syn/Anti)
- Stereoselective and Stereospecific Reactions
- Hydrohalogenation of Alkenes and Markovnikov's Rule
- Hydration of Alkenes With Aqueous Acid
- Rearrangements in Alkene Addition Reactions
- Halogenation of Alkenes and Halohydrin Formation
- Oxymercuration Demercuration of Alkenes
- Hydroboration Oxidation of Alkenes
- m-CPBA (meta-chloroperoxybenzoic acid)
- OsO4 (Osmium Tetroxide) for Dihydroxylation of Alkenes
- Palladium on Carbon (Pd/C) for Catalytic Hydrogenation of Alkenes
- Cyclopropanation of Alkenes
- A Fourth Alkene Addition Pattern - Free Radical Addition
- Alkene Reactions: Ozonolysis
- Summary: Three Key Families Of Alkene Reaction Mechanisms
- Synthesis (4) - Alkene Reaction Map, Including Alkyl Halide Reactions
- Alkene Reactions Practice Problems
13 Alkyne Reactions
- Acetylides from Alkynes, And Substitution Reactions of Acetylides
- Partial Reduction of Alkynes With Lindlar's Catalyst
- Partial Reduction of Alkynes With Na/NH3 To Obtain Trans Alkenes
- Alkyne Hydroboration With "R2BH"
- Hydration and Oxymercuration of Alkynes
- Hydrohalogenation of Alkynes
- Alkyne Halogenation: Bromination and Chlorination of Alkynes
- Oxidation of Alkynes With O3 and KMnO4
- Alkenes To Alkynes Via Halogenation And Elimination Reactions
- Alkynes Are A Blank Canvas
- Synthesis (5) - Reactions of Alkynes
- Alkyne Reactions Practice Problems With Answers
14 Alcohols, Epoxides and Ethers
- Alcohols - Nomenclature and Properties
- Alcohols Can Act As Acids Or Bases (And Why It Matters)
- Alcohols - Acidity and Basicity
- The Williamson Ether Synthesis
- Ethers From Alkenes, Tertiary Alkyl Halides and Alkoxymercuration
- Alcohols To Ethers via Acid Catalysis
- Cleavage Of Ethers With Acid
- Epoxides - The Outlier Of The Ether Family
- Opening of Epoxides With Acid
- Epoxide Ring Opening With Base
- Making Alkyl Halides From Alcohols
- Tosylates And Mesylates
- PBr3 and SOCl2
- Elimination Reactions of Alcohols
- Elimination of Alcohols To Alkenes With POCl3
- Alcohol Oxidation: "Strong" and "Weak" Oxidants
- Demystifying The Mechanisms of Alcohol Oxidations
- Protecting Groups For Alcohols
- Thiols And Thioethers
- Calculating the oxidation state of a carbon
- Oxidation and Reduction in Organic Chemistry
- Oxidation Ladders
- SOCl2 Mechanism For Alcohols To Alkyl Halides: SN2 versus SNi
- Alcohol Reactions Roadmap (PDF)
- Alcohol Reaction Practice Problems
- Epoxide Reaction Quizzes
- Oxidation and Reduction Practice Quizzes
15 Organometallics
- What's An Organometallic?
- Formation of Grignard and Organolithium Reagents
- Organometallics Are Strong Bases
- Reactions of Grignard Reagents
- Protecting Groups In Grignard Reactions
- Synthesis Problems Involving Grignard Reagents
- Grignard Reactions And Synthesis (2)
- Organocuprates (Gilman Reagents): How They're Made
- Gilman Reagents (Organocuprates): What They're Used For
- The Heck, Suzuki, and Olefin Metathesis Reactions (And Why They Don't Belong In Most Introductory Organic Chemistry Courses)
- Reaction Map: Reactions of Organometallics
- Grignard Practice Problems
16 Spectroscopy
- Degrees of Unsaturation (or IHD, Index of Hydrogen Deficiency)
- Conjugation And Color (+ How Bleach Works)
- Introduction To UV-Vis Spectroscopy
- UV-Vis Spectroscopy: Absorbance of Carbonyls
- UV-Vis Spectroscopy: Practice Questions
- Bond Vibrations, Infrared Spectroscopy, and the "Ball and Spring" Model
- Infrared Spectroscopy: A Quick Primer On Interpreting Spectra
- IR Spectroscopy: 4 Practice Problems
- 1H NMR: How Many Signals?
- Homotopic, Enantiotopic, Diastereotopic
- Diastereotopic Protons in 1H NMR Spectroscopy: Examples
- 13-C NMR - How Many Signals
- Liquid Gold: Pheromones In Doe Urine
- Natural Product Isolation (1) - Extraction
- Natural Product Isolation (2) - Purification Techniques, An Overview
- Structure Determination Case Study: Deer Tarsal Gland Pheromone
17 Dienes and MO Theory
- What To Expect In Organic Chemistry 2
- Are these molecules conjugated?
- Conjugation And Resonance In Organic Chemistry
- Bonding And Antibonding Pi Orbitals
- Molecular Orbitals of The Allyl Cation, Allyl Radical, and Allyl Anion
- Pi Molecular Orbitals of Butadiene
- Reactions of Dienes: 1,2 and 1,4 Addition
- Thermodynamic and Kinetic Products
- More On 1,2 and 1,4 Additions To Dienes
- s-cis and s-trans
- The Diels-Alder Reaction
- Cyclic Dienes and Dienophiles in the Diels-Alder Reaction
- Stereochemistry of the Diels-Alder Reaction
- Exo vs Endo Products In The Diels Alder: How To Tell Them Apart
- HOMO and LUMO In the Diels Alder Reaction
- Why Are Endo vs Exo Products Favored in the Diels-Alder Reaction?
- Diels-Alder Reaction: Kinetic and Thermodynamic Control
- The Retro Diels-Alder Reaction
- The Intramolecular Diels Alder Reaction
- Regiochemistry In The Diels-Alder Reaction
- The Cope and Claisen Rearrangements
- Electrocyclic Reactions
- Electrocyclic Ring Opening And Closure (2) - Six (or Eight) Pi Electrons
- Diels Alder Practice Problems
- Molecular Orbital Theory Practice
18 Aromaticity
- Introduction To Aromaticity
- Rules For Aromaticity
- Huckel's Rule: What Does 4n+2 Mean?
- Aromatic, Non-Aromatic, or Antiaromatic? Some Practice Problems
- Antiaromatic Compounds and Antiaromaticity
- The Pi Molecular Orbitals of Benzene
- The Pi Molecular Orbitals of Cyclobutadiene
- Frost Circles
- Aromaticity Practice Quizzes
19 Reactions of Aromatic Molecules
- Electrophilic Aromatic Substitution: Introduction
- Activating and Deactivating Groups In Electrophilic Aromatic Substitution
- Electrophilic Aromatic Substitution - The Mechanism
- Ortho-, Para- and Meta- Directors in Electrophilic Aromatic Substitution
- Understanding Ortho, Para, and Meta Directors
- Why are halogens ortho- para- directors?
- Disubstituted Benzenes: The Strongest Electron-Donor "Wins"
- Electrophilic Aromatic Substitutions (1) - Halogenation of Benzene
- Electrophilic Aromatic Substitutions (2) - Nitration and Sulfonation
- EAS Reactions (3) - Friedel-Crafts Acylation and Friedel-Crafts Alkylation
- Intramolecular Friedel-Crafts Reactions
- Nucleophilic Aromatic Substitution (NAS)
- Nucleophilic Aromatic Substitution (2) - The Benzyne Mechanism
- Reactions on the "Benzylic" Carbon: Bromination And Oxidation
- The Wolff-Kishner, Clemmensen, And Other Carbonyl Reductions
- More Reactions on the Aromatic Sidechain: Reduction of Nitro Groups and the Baeyer Villiger
- Aromatic Synthesis (1) - "Order Of Operations"
- Synthesis of Benzene Derivatives (2) - Polarity Reversal
- Aromatic Synthesis (3) - Sulfonyl Blocking Groups
- Birch Reduction
- Synthesis (7): Reaction Map of Benzene and Related Aromatic Compounds
- Aromatic Reactions and Synthesis Practice
- Electrophilic Aromatic Substitution Practice Problems
20 Aldehydes and Ketones
- What's The Alpha Carbon In Carbonyl Compounds?
- Nucleophilic Addition To Carbonyls
- Aldehydes and Ketones: 14 Reactions With The Same Mechanism
- Sodium Borohydride (NaBH4) Reduction of Aldehydes and Ketones
- Grignard Reagents For Addition To Aldehydes and Ketones
- Wittig Reaction
- Hydrates, Hemiacetals, and Acetals
- Imines - Properties, Formation, Reactions, and Mechanisms
- All About Enamines
- Breaking Down Carbonyl Reaction Mechanisms: Reactions of Anionic Nucleophiles (Part 2)
- Aldehydes Ketones Reaction Practice
21 Carboxylic Acid Derivatives
- Nucleophilic Acyl Substitution (With Negatively Charged Nucleophiles)
- Addition-Elimination Mechanisms With Neutral Nucleophiles (Including Acid Catalysis)
- Basic Hydrolysis of Esters - Saponification
- Transesterification
- Proton Transfer
- Fischer Esterification - Carboxylic Acid to Ester Under Acidic Conditions
- Lithium Aluminum Hydride (LiAlH4) For Reduction of Carboxylic Acid Derivatives
- LiAlH[Ot-Bu]3 For The Reduction of Acid Halides To Aldehydes
- Di-isobutyl Aluminum Hydride (DIBAL) For The Partial Reduction of Esters and Nitriles
- Amide Hydrolysis
- Thionyl Chloride (SOCl2) And Conversion of Carboxylic Acids to Acid Halides
- Diazomethane (CH2N2)
- Carbonyl Chemistry: Learn Six Mechanisms For the Price Of One
- Making Music With Mechanisms (PADPED)
- Carboxylic Acid Derivatives Practice Questions
22 Enols and Enolates
- Keto-Enol Tautomerism
- Enolates - Formation, Stability, and Simple Reactions
- Kinetic Versus Thermodynamic Enolates
- Aldol Addition and Condensation Reactions
- Reactions of Enols - Acid-Catalyzed Aldol, Halogenation, and Mannich Reactions
- Claisen Condensation and Dieckmann Condensation
- Decarboxylation
- The Malonic Ester and Acetoacetic Ester Synthesis
- The Michael Addition Reaction and Conjugate Addition
- The Robinson Annulation
- Haloform Reaction
- The Hell–Volhard–Zelinsky Reaction
- Enols and Enolates Practice Quizzes
23 Amines
- The Amide Functional Group: Properties, Synthesis, and Nomenclature
- Basicity of Amines And pKaH
- 5 Key Basicity Trends of Amines
- The Mesomeric Effect And Aromatic Amines
- Nucleophilicity of Amines
- Alkylation of Amines (Sucks!)
- Reductive Amination
- The Gabriel Synthesis
- Some Reactions of Azides
- The Hofmann Elimination
- The Hofmann and Curtius Rearrangements
- The Cope Elimination
- Protecting Groups for Amines - Carbamates
- The Strecker Synthesis of Amino Acids
- Introduction to Peptide Synthesis
- Reactions of Diazonium Salts: Sandmeyer and Related Reactions
- Amine Practice Questions
24 Carbohydrates
- D and L Notation For Sugars
- Pyranoses and Furanoses: Ring-Chain Tautomerism In Sugars
- What is Mutarotation?
- Reducing Sugars
- The Big Damn Post Of Carbohydrate-Related Chemistry Definitions
- The Haworth Projection
- Converting a Fischer Projection To A Haworth (And Vice Versa)
- Reactions of Sugars: Glycosylation and Protection
- The Ruff Degradation and Kiliani-Fischer Synthesis
- Isoelectric Points of Amino Acids (and How To Calculate Them)
- Carbohydrates Practice
- Amino Acid Quizzes
25 Fun and Miscellaneous
- A Gallery of Some Interesting Molecules From Nature
- Screw Organic Chemistry, I'm Just Going To Write About Cats
- On Cats, Part 1: Conformations and Configurations
- On Cats, Part 2: Cat Line Diagrams
- On Cats, Part 4: Enantiocats
- On Cats, Part 6: Stereocenters
- Organic Chemistry Is Shit
- The Organic Chemistry Behind "The Pill"
- Maybe they should call them, "Formal Wins" ?
- Why Do Organic Chemists Use Kilocalories?
- The Principle of Least Effort
- Organic Chemistry GIFS - Resonance Forms
- Reproducibility In Organic Chemistry
- What Holds The Nucleus Together?
- How Reactions Are Like Music
- Organic Chemistry and the New MCAT
26 Organic Chemistry Tips and Tricks
- Common Mistakes: Formal Charges Can Mislead
- Partial Charges Give Clues About Electron Flow
- Draw The Ugly Version First
- Organic Chemistry Study Tips: Learn the Trends
- The 8 Types of Arrows In Organic Chemistry, Explained
- Top 10 Skills To Master Before An Organic Chemistry 2 Final
- Common Mistakes with Carbonyls: Carboxylic Acids... Are Acids!
- Planning Organic Synthesis With "Reaction Maps"
- Alkene Addition Pattern #1: The "Carbocation Pathway"
- Alkene Addition Pattern #2: The "Three-Membered Ring" Pathway
- Alkene Addition Pattern #3: The "Concerted" Pathway
- Number Your Carbons!
- The 4 Major Classes of Reactions in Org 1
- How (and why) electrons flow
- Grossman's Rule
- Three Exam Tips
- A 3-Step Method For Thinking Through Synthesis Problems
- Putting It Together
- Putting Diels-Alder Products in Perspective
- The Ups and Downs of Cyclohexanes
- The Most Annoying Exceptions in Org 1 (Part 1)
- The Most Annoying Exceptions in Org 1 (Part 2)
- The Marriage May Be Bad, But the Divorce Still Costs Money
- 9 Nomenclature Conventions To Know
- Nucleophile attacks Electrophile
27 Case Studies of Successful O-Chem Students
- Success Stories: How Corina Got The The "Hard" Professor - And Got An A+ Anyway
- How Helena Aced Organic Chemistry
- From a "Drop" To B+ in Org 2 – How A Hard Working Student Turned It Around
- How Serge Aced Organic Chemistry
- Success Stories: How Zach Aced Organic Chemistry 1
- Success Stories: How Kari Went From C– to B+
- How Esther Bounced Back From a "C" To Get A's In Organic Chemistry 1 And 2
- How Tyrell Got The Highest Grade In Her Organic Chemistry Course
- This Is Why Students Use Flashcards
- Success Stories: How Stu Aced Organic Chemistry
- How John Pulled Up His Organic Chemistry Exam Grades
- Success Stories: How Nathan Aced Organic Chemistry (Without It Taking Over His Life)
- How Chris Aced Org 1 and Org 2
- Interview: How Jay Got an A+ In Organic Chemistry
- How to Do Well in Organic Chemistry: One Student's Advice
- "America's Top TA" Shares His Secrets For Teaching O-Chem
- "Organic Chemistry Is Like..." - A Few Metaphors
- How To Do Well In Organic Chemistry: Advice From A Tutor
- Guest post: "I went from being afraid of tests to actually looking forward to them".
this was so helpful. now wondering why i didnt just come here in the first place i could have gotten an a plus for my organic chemistry exam
Plz give one suggestion to me
Malic acid , specific optical rotation (-0.1 to +0.1) why
and what are meaning of (-0.1 to +0.1) in subjected specific optical rotation
plz suggeste to me
with regards
Ajay k. Maurya
Hi! I’m still confused with one thing. Are diastereomers always optically active? When is it not and when is it active?
Whether a molecule is optically active is an independent property relative to whether or not it has a diastereomer.
For example cis and trans 2-butene are diastereomers, but the molecules are achiral, because each molecule has a plane of symmetry (in the plane of the page).
That’s the key thing when determining whether or not a molecule is capable of being optically active. Does it have a plane of symmetry?
Generally, a molecule with only one chiral center will not have a plane of symmetry, and therefore can be optically active.
Most molecules with two chiral centers also lack a plane of symmetry, and are therefore optically active, but you need to *watch out* for meso compounds, because these are molecules which have 2 (or more) chiral centers but are arranged in such a way that the molecule lacks a plane of symmetry.
(Just one last point. Don’t forget that the terms “enanantiomers”, “diastereomers”, etc. are about relationships between two molecules, just like “brother”, “cousin”, “father” are relationships between people. It’s possible for a molecule to be both an enantiomer of one molecule and a diastereomer of another, just like it’s possible for a person to be both a brother to one person and a father to another. That’s why I say that physical properties like optical rotation are independent of those terms.)
we are getting the Specific optical rotation results exact double against the limit what are probable reason as we have cross checked all the parameters but unable to find out the root cause.
If you had a sample volume of 2.62 mL and the cell was 12.5 cm, the cross-sectional area of the tube would be about 0.2 cm^2 and its diameter would be about 5 mm. Do people often do polarimetry in NMR tubes?
Ha! That is a great point Dave!
The pure sample of the R isomer of a compound has [𝛼] = +5.756°. If you will prepare a
solution with 0.300 mol of the R isomer, and 0.700 mol of the S isomer, what will be your
prediction of the [𝛼] of the solution?
Was having a problem with this question in a textbook:
“If a solution of a compound has a rotation of +12, how could
you tell if this was actually +12, or really –348, or +372?”
For which the solution implies using [a] = a / cl & changing concentration should enable you to deduce the answer. But I’m not quite seeing how, would you be able to explain please?
Dilute it by half. You will either get +6 or +181.
Hi Dale,
I was wondering if there is a difference in specific rotation between anhydrous and monohydrous salt forms of a drug substance. If yes, how can this be calculated?
Do you have a specific example?
So from this (and my textbook) it seems there is no direct correlation between (S), (R) and optical rotation correct? I thought I had this all in hand but I got the following question incorrect on my exam “If (S)-2-ethyl-1-hexanol has a specific rotation of -20.05 degrees, what is the specific rotation of (R)-2-ethyl-1-hexanol?”. I don’t know what the correct answer would be in this case, can you help?
Hi Sarah – Between any random molecule with (S) and any random molecule with (R) you are right that there is no simple correlation to the direction of rotation of polarized light.
However these two molecules are not just any random molecule! The key part of this question is recognizing that (S)-2-ethyl-1-hexanol and (R)-2-ethyl-1-hexanol are *enantiomers*.
It is true that enantiomers rotate plane-polarized light to exactly equal and opposite extents. That’s why racemic mixtures don’t rotate polarized light – the rotations cancel out.
Therefore if (S) has a specific rotation of -20.05 degrees, the specific rotation of (R) will be +20.05 degrees.
I got the polarimeter reading as -0.039 for jasmine essential oil. so how do i calculate Optical rotation and specific rotation.
Essential oils are usually complex mixtures of terpenes. Are you dealing with a pure compound? If not, optical rotation is useless.
Am finding 15.31 after computing! Is there a mistake in your calculation?
Yes. Fixed. Thank you for spotting the error!
In the above-titled section on your website, you state “For example, for (S)-malic acid at a concentration of 5.5 g/ mL in the solvent pyridine….”. This concentration cannot be correct. If you combine 5.5 g malic acid (or almost any solid) with only 1 mL of pyridine (or almost any solvent), you will get a sticky mess. Furthermore, 5.5 g of malic acid is 0.041 mol of acid while 1 mL of pyridine is 0.0124 mol of base, so 0.0124 mol pyridine will simply react with 0.0124 mol of malic acid, make 0.0124 mol of a salt and probably just solidify in the rest of the malic acid. Shoud the concentration be 5.5 g/L or 0.55 g/mL?
Shouldn’t it be 5.5 g malic acid/100 mL pyridine? I know for pure liquids the unit is g/mL while for solutions, it’s g/100 mL
That is correct. I’ve updated the article to reflect this. Thank you very much.
Hey there!
I did an experiment where i increased the concentration of sugar in a sugar-water solution and calculated the observed angles. I used a different wavelength than D and the temp was about 30 deg C and a pathlength of about 25 cm. I graphed concentration vs angle to find a linear relationship as expected. However, i checked and the specific rotation of sugar (sucrose) is +66. However, when i put my observed angles and concentrations into the equation (about 11 deg at 25g/100mL water), my specific rotation was much lower. Is this normal? Also how do i use the slope of my graph to find out the specific rotation? Do i have to put the individual points into the equation one by one or can is there a way where I can just use the slope? What can I do with this graph?
if single bond rotates, why glucose does not get converted into mannose or other structural isomers??
Because glucose and mannose have different *configurations*. Rotating a single bond does not change the configuration of glucose, in the same way that no amount of wiggling your left hand will turn it into your right hand.
In this case (for historical reasons), c = 1.0 translates to 10 mg of sample in 1.0 ml of solvent.
I believe in the sample problem you have made the incorrect calculation Note the added parentheses in the equation. It should be:
[α] = [+ 9.06° ] / [(1.24 g/ 2.62 mL) x 1.25 dm]
[α] = +15.3
That is correct. My mistake. I greatly appreciate the correction Dale.
“For example, for (S)-malic acid at a concentration of 5.5 g/ mL in the solvent pyridine at 20°C at a wavelength of 589 nm, the specific rotation is –27° . We can describe this in shorthand as [α]20D –27° (c = 5.5, pyridine)”
How does one get 5.5 grams into one mL ? So what does c=5.5 actually mean?
Since there is no direct correlation between R and S and the optical rotation of a chiral compound.
To check the chirality of a chiral compound, the specific rotation is measured on the polarimeter, using a specified solvent. Then can the specific rotation result be used for confirmation of the R or S configuration of the molecule?
5.5 is g/100mL
Yes, thank you.