Staggered vs Eclipsed Conformations of Ethane

Staggered vs Eclipsed Conformations of Ethane, or Why Newman Projections Are Awesome

The three-dimensional shape of methane (CH₄) is the same under all conditions, but ethane (C₂H₆) and higher alkanes can assume different three-dimensional shapes due to rotation along the C-C bond.

In this article: introducing conformational isomers, staggered and eclipsed conformations, the Newman projection, the dihedral angle (torsion angle), and the rotational barrier to ethane (torsional strain)!

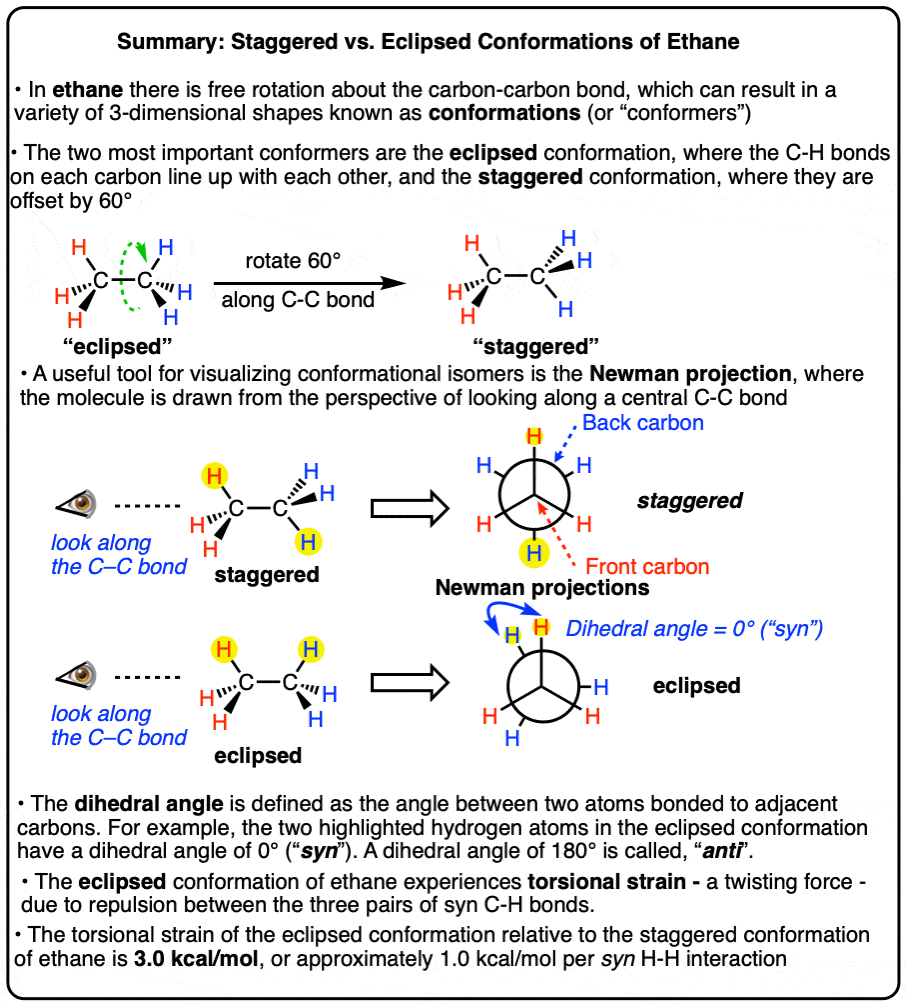
Table of Contents

1. Recap: The Tetrahedral Structure of Methane (CH₄)
2. The Three-Dimensional Structure of Ethane (C₂H₆)
3. Rotations Along Carbon-Carbon Bonds: Conformational Isomers Of Ethane
4. Eclipsed And Staggered Conformations Of Ethane
5. The Newman Projection of Ethane
6. The Dihedral Angle, Or Torsion Angle
7. Mapping Out The Conformations Of Ethane By Dihedral Angle
8. Torsional Strain
9. Notes
10. Quiz Yourself!
11. (Advanced) References and Further Reading

1. Recap: The Tetrahedral Structure of Methane (CH₄)

In a previous post we discussed how we know that methane CH₄ is tetrahedral (See: How Do We Know That Methane Is Tetrahedral), as this shape maximizes the distance between the repulsive bonding electron pairs.

We also saw that CH₄ is a perfect tetrahedron, with H-C-H bond angles of 109.5 °.

To depict methane in three dimensions, it’s customary to draw two of the C–H bonds with full lines to depict the C–H bonds in the plane of the page. The C–H bond pointing out of the page is drawn with a “wedge” (heavy) bond, and the C–H bond pointing into (behind) the page is drawn with a “dashed” bond.

This convention borrows an old artists’ trick: to give the illusion of perspective,  depict objects in the foreground with high-contrast (heavy lines), and objects in the background with low contrast (faint lines).
Hover here for a pop-up image .

Here’s are two “line-wedge” drawings of CH₄. Both of these drawings depict the same three dimensional object.

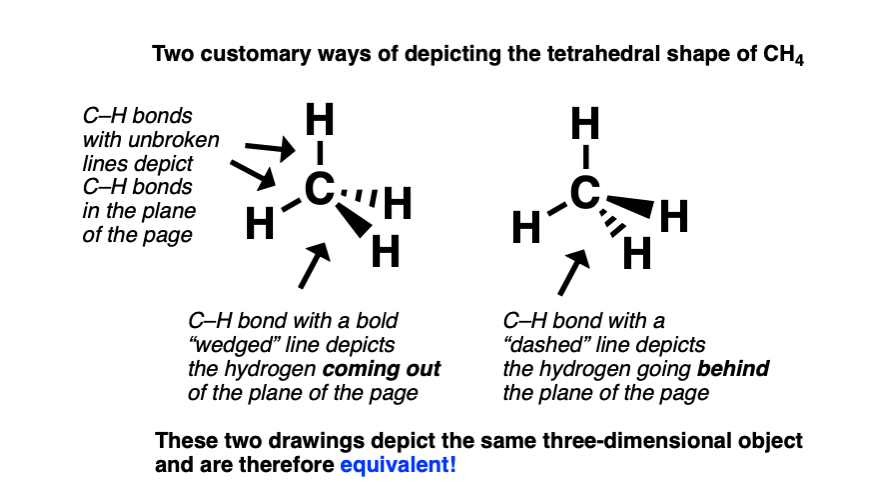
Does it matter whether the “wedged” bond is drawn below or above the “dashed” bond?

No. Whether or not the wedge is drawn below or above the dash is just a matter of perspective, depicting what you’d see if you were looking “down on” or “up to” the CH₄ molecule.

via GIPHY

Many other perspective drawings of methane are possible,  the perspective where two C-H bonds are in the plane of the page has the most utility. It clearly depicts all atoms arranged tetrahedrally about the central carbon, involves the least amount of work,  and therefore tends to be the standard way to depict these molecules.

Very rarely, it’s useful to show other perspectives of CH₄. For instance, did you know that when you look along one of the C–H bonds, it makes the other C-H bonds look like they are separated by angles of 120° ?

Note: to be clear, the H–C–H bond angle is still 109.5°. What’s being said here is that in this perspective, the three hydrogens trace out a circle, with an angle of 120° separating them). 

More on that in a moment.

2. The Three-Dimensional Structure of Ethane (C₂H₆)

So if that’s the structure of methane (CH₄) then what is the structure of the next hydrocarbon up, ethane (C₂H₆) ?

All we need to do is replace one of the C-H bonds of methane with a bond to a CH₃ (“methyl”) fragment.

Both carbons remain tetrahedral.

There’s several ways to draw it using a bond-line diagram. Two of them are drawn below.

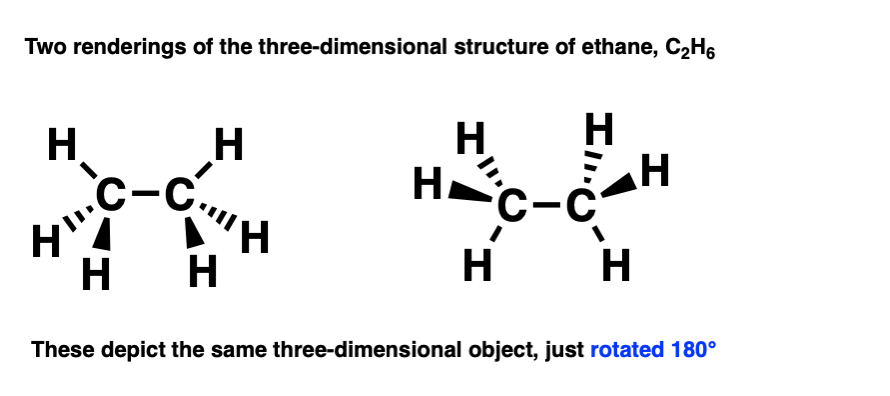
Molecules are 3-dimensional objects. Note that these drawings both depict the same molecule, but are drawn from different perspectives.

This becomes clear if you rotate the molecule by 180 degrees.

By building a model of them both, by rotating one of them 180 degrees we can see that they are the same thing.

via GIPHY

An important point: In chemistry, if two molecules can be superimposed on each other, that means that they are the same molecule.

3. Rotations Along Carbon-Carbon Bonds: Conformational Isomers Of Ethane

The addition of the new carbon-carbon bond in ethane brings about some additional complications that are part of what makes organic chemistry interesting (or as some of us like to say, “fun”).

Methane has the same three-dimensional shape at all times. We can draw it from a number of perspectives, but it retains the same shape.

This is not true of ethane!

The two CH₃ fragments are joined by a carbon-carbon sigma bond. The connection of two atoms through a sigma bond is like connecting two Lego pieces through a single “stud” and “tube”.  Rotation can occur along the bond without disrupting the connection.

This rotation about the C-C bond can give rise to a variety of 3-dimensional shapes.

These different shapes are called, “conformations“, or, “conformational isomers“, or sometimes, “rotational isomers (rotamers)”.

That means that a second, perfectly valid, way to draw ethane, is like this:

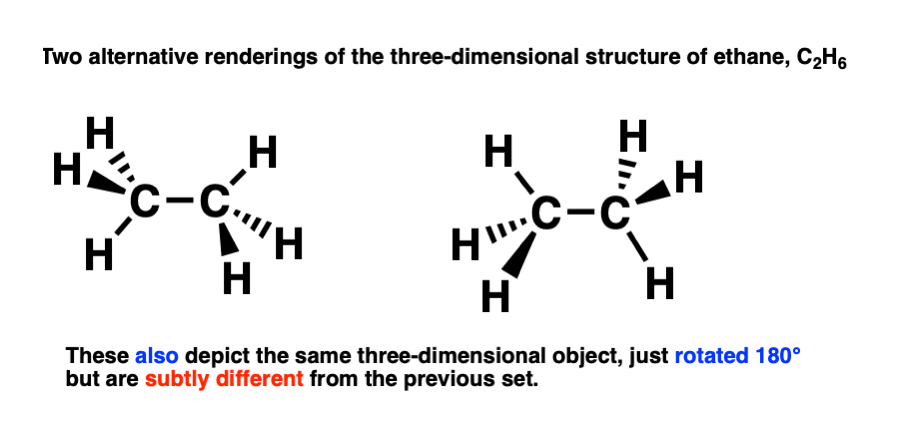
This is a conformational isomer of the drawing of ethane we made previously (above).

The difference is subtle! These two conformational isomers can be interconverted by rotating the carbon-carbon bond 60 degrees, like this:

via GIPHY

So the two conformational isomers represent the same molecule, but a different three-dimensional shape.

[These shapes also have subtle differences in energies – more on that in a moment. ]

4. Eclipsed And Staggered Conformations Of Ethane

In case it’s still not obvious to you how these two forms of ethane are subtly different, it might help to look at it end-on.

Let’s take the first drawing of ethane, and look along the C–C bond from the right hand side. In order to show this, we often use little symbol that is intended to look like an eye, along with an arrow showing the direction in which the “eye” is looking. Think of it as, “side-eye”.

When apply this “side-eye”,  we get this:

via GIPHY

Note that the three hydrogens on the front carbon are directly in front of the three hydrogens in the back.

We call this the “eclipsed” conformation.

The “end-on” perspective shown in the video is a Newman projection – more on that in a second.

Now let’s take the second drawing of ethane, and look along the C–C bond from the right-hand side.

via GIPHY

In this case, note that all the hydrogens are spaced out 60 degrees from each other.

This is referred to as the “staggered” conformation.

An important note. When we discuss “eclipsed” and “staggered” we are referring to the relationship of all three substituents in the front carbon to all three substituents in the back carbon.

This is in contrast to the dihedral angle (e.g. “syn” and “anti” relationships, discussed below) where we are comparing the orientation of one substituent on the front carbon with respect to one substituent on the back carbon.

5.  Visualizing Staggered vs Eclipsed Conformations of Ethane: Introducing The Newman Projection

As you probably noticed, the “end-on” views of the staggered and eclipsed conformations in the short videos above were drawn in a quirky way. What’s the deal with those circles?

These are Newman projections, a useful visual aid for comparing conformational isomers, named after their proponent, Melvin S. Newman of Ohio State University. [Note 2]

A Newman projection is a perspective drawing of a molecule looking “end on” along one of the bonds. It wasn’t the first proposal [Note 3] for this perspective, but it’s become the industry standard.

The “circle” is meant to depict the atom in the foreground which blocks the view of the carbon in the background.

In the case of ethane, there’s really only interesting bond to look along: the carbon-carbon bond.

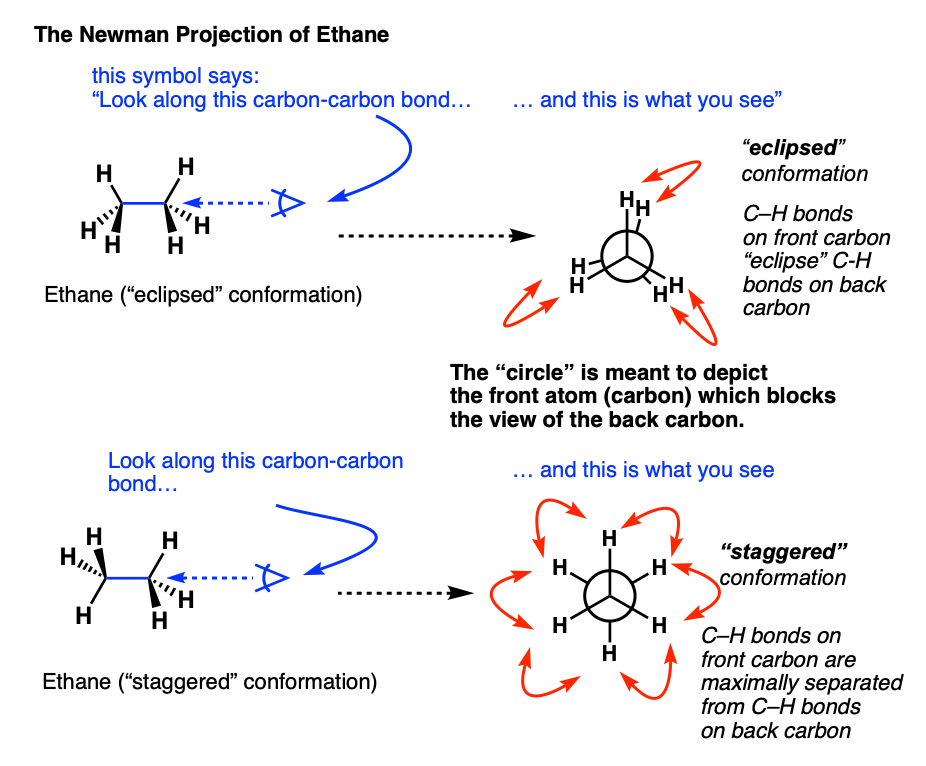
Rather than consider every conformation (there are an infinite number), it greatly simplifies discussion if we to just consider the two extremes in ethane – when the C-H bonds on the neighboring carbons are at their minimum distance from each other (0°, eclipsed) or their maximum distance away from each other (60°, staggered).

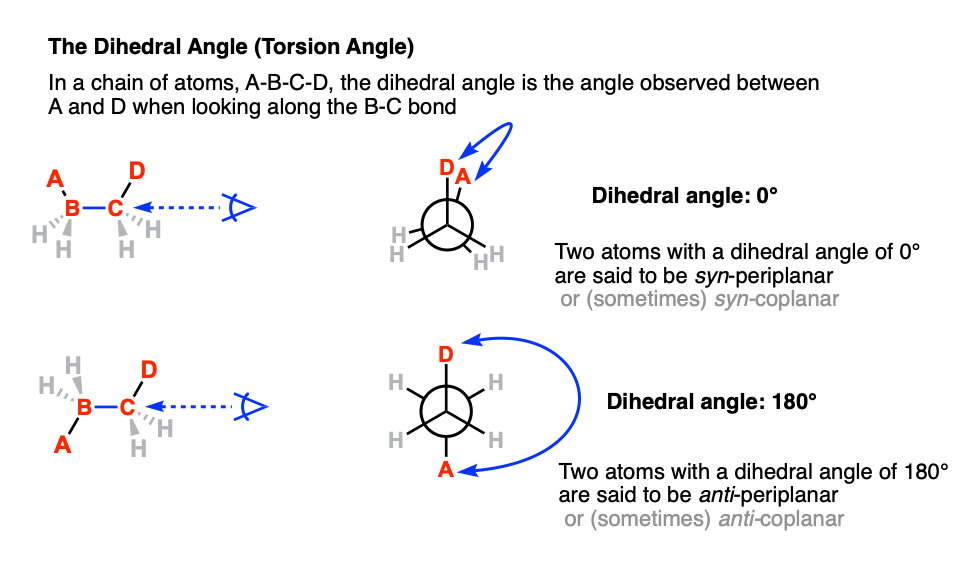
6. The Dihedral Angle (Or Torsion Angle)

As a wise person once said, perspective is worth 80 IQ points.

The genius of the Newman projection is that the “end-on” perspective makes analysis of the spatial relationships between the front and back groups much more obvious.

The dihedral angle [also: torsion angle] is defined as the angle made between the four atoms A-B-C-D when looking along the B-C bond.

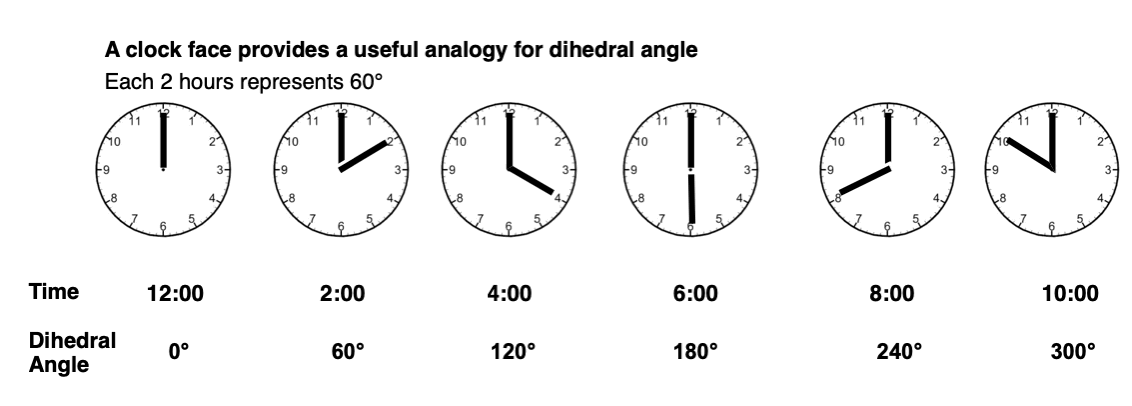
A clock face is a useful analogy. At 12:00, the dihedral angle is 0°. Every hour represents 30°. For the purposes of tetrahedral carbon, 30° is not very interesting (it’s doesn’t lead to an energy maximum or minimum) so let’s employ 2-hour increments instead.

Among all the possible angles, the term syn refers to the situation when the two atoms are on the same side of the “equator” (dihedral angle +90° ≥ 0° ≤ –90°).  and the term “anti” refers to the situation when the two atoms are on opposite sides of the equator (dihedral angle (+90° ≤ 180° ≥ –90°)

The term “periplanar” refers to the situation when the dihedral angle of the two atoms are parallel (0°, or 12:00 in our clock analogy) or antiparallel (180°, or 6:00).

7. Mapping Out The Conformations Of Ethane By Dihedral Angle

Let’s try this with ethane.

In order to define a torsion angle, we need to arbitrarily select two of the C-H bonds on the neighboring carbons to be our reference points.

Let’s start with the two H atoms highlighted in red, with a dihedral angle of 0° (12:00 in our clock analogy).

If we start at 12:00, and keep the front CH₃ in the same place while rotating the “back” CH₃ in 60 degree increments, ,we get something like this:

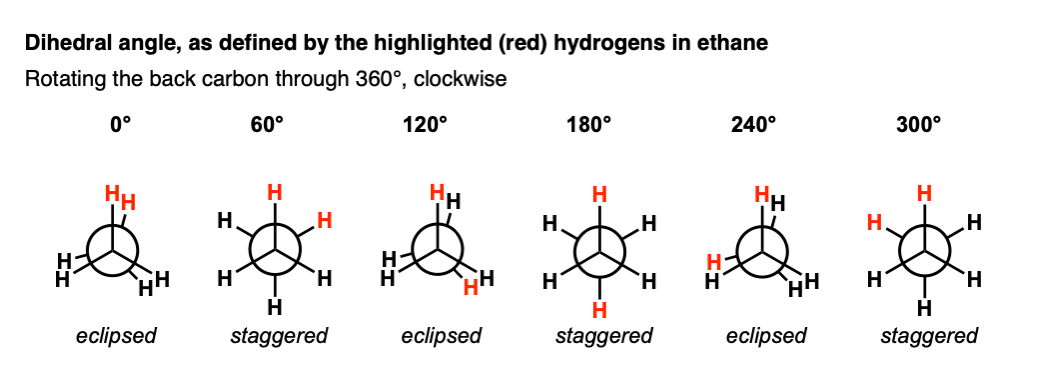
It bears repeating:  staggered and eclipsed refers to the orientation of the front 3 groups with respect to the back 3 bonds.

This is different than the dihedral angle, which in this case refers to the angle made by H–C–C–H when looking along the C–C bond.

Here’s a quick movie of what that looks like on a Newman.

via GIPHY

There’s really only two important conformations of ethane, and they repeat themselves 3 times as we rotate the C–C bond through 360°.

8. Torsional Strain

So are the two important conformational isomers of ethane equivalent in energy?

Great question!

No they are not. As discovered by Kemp and Pitzer in 1936 [ref], the two conformations differ in energy by about 3.0 kcal/mol and the energy difference can be measured through a variety of techniques (see here).

The staggered conformation is lower in energy than the eclipsed conformation.

This means that there is a small barrier to rotation of about 3.0 kcal/mol. [Note 6] This barrier isn’t big enough to prevent “free” rotation about the C-C bond, but it does mean that the staggered and eclipsed conformations will be present in different amounts (with the staggered predominating).

[The classic reason stated for the barrier to rotation is  Van der Waals repulsion of the C–H bonds on the adjacent carbons in the eclipsed conformation. Others favor a “hyperconjugation” explanation. Further reading in the references [1 2] for the curious].

With this information in hand, we can make a graph of dihedral angle versus energy that looks like this:

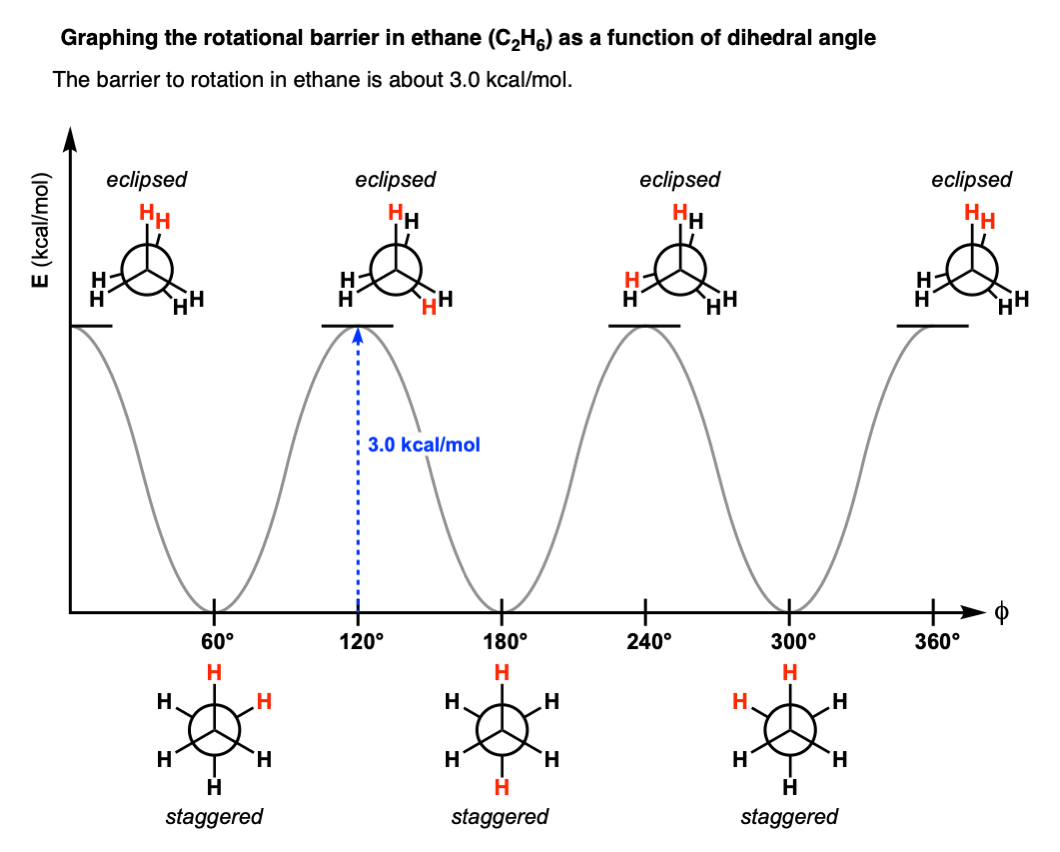
As the C–C bond undergoes rotation such that the molecule goes from a staggered to an eclipsed conformation, the molecule experiences strain.

This type of strain is called torsional strain, eclipsing strain, or Pitzer strain, depending on who you talk to. [Note 5]

The term “torsional strain” is an analogy to the twisting force one experiences when you twist a spring or (more commonly) a rubber band – for instance, in a rubber-band driven propeller plane.

That force you feel that makes the elastic want to “unwind” is a form of torsional strain.

9. What About Propane and Butane?

Let’s summarize:

• Molecules are three-dimensional objects like so many other things in our daily experience
• They can be drawn from a variety of perspectives. Changing the perspective does not change the molecule, but it can help to visualize certain characteristics.
• Two molecules that are superimposable are the same molecule!
• Complicating the depiction of molecules more complex than methane is the existence of free rotation about the carbon-carbon bond, leading to conformational isomers – the same molecule, but with different 3-dimensional shapes
• Conformational isomers are interconvertible through bond rotations. Interconversion is extremely fast and happens billions of times per second.
• There are two important conformations in ethane: the eclipsed and the staggered conformation
• The Newman projection is a useful conceptual tool for visualizing conformations
• When looking at a Newman projection, the dihedral angle is defined as the angle made between two designated atoms on the front and back carbons.
• Staggered and eclipsed refer the relative orientation of all the bonds on the front carbon versus all the bonds on the back carbon. The dihedral angle and its encompassing terms (syn, anti, periplanar) refer to the relationship between one individual bond on the front carbon versus one individual bond on the back carbon.
• The barrier to rotation in ethane is about 3.0 kcal/mol and the staggered conformation is the lowest-energy conformation
• The term used to refer to this barrier to rotation is torsional strain

So what about higher alkanes? As you expect, things get a little bit more complicated…  but it’s really not too bad.

In the next article we’ll look at the conformations of the next alkane up,  propane (CH₃CH₂CH₃)

Notes

Note 1. Another depiction of CH₄ that is worth noting is the Fischer projection, where the horizontal bonds are wedges that “come out to hug you”, and the vertical bonds are “dashes” that point behind the page.

Note 2. Here’s a screenshot of the original Newman paper.

Here’s the Newman projections from this paper.

Note 3. The Newman was not the first attempt to show this perspective. For some reason the Hermans and Bischoff projections never took off. Source.

Note 4. Technically, the dihedral angle [IUPAC] refers to the angle between two planes, and the torsion angle [IUPAC] is the dihedral angle of the A-B-C and B-C-D planes in the four-bond system A-B-C-D. Dihedral angle is a broader definition. For our purposes, we’ll treat them as equivalent terms.

Note 5. IUPAC has decided to replace “Torsional Strain” and “Pitzer strain” with “Eclipsing Strain“. The chance of this preventing people using these terms in everyday lab parlance is zero.

Note 6.  Since the torsional strain in ethane is about 3.0 kcal/mol, that would imply that each C–H eclipsing interaction is worth about 1.0 kcal/mol. In CH₃-NH₂ the eclipsed conformation is about 1.98 kcal/mol above the staggered conformation, and in CH₃-OH the eclipsed conformation is about 1.07 kcal/mol above the staggered conformation, so these results broadly agree with the “1 kcal/mol per eclipsing C-H bond” result.

Quiz Yourself!

Click to Flip

Click to Flip

(Advanced) References and Further Reading

1. The Entropy of Ethane and the Third Law of Thermodynamics. Hindered Rotation of Methyl Groups
   J. D. Kemp and Kenneth S. Pitzer
   Journal of the American Chemical Society 1937 59 (2), 276-279
   DOI: 10.1021/ja01281a014
   The first report of the barrier to rotation in ethane.
2. The Infrared Spectrum of C2H6
   Lincoln G. Smith
   J. Chem. Phys. 17, 139, (1949)
   DOI: 10.1063/1.1747206
   In this paper it was determined for the first time that the staggered conformation of ethane is the lowest in energy, by measuring the infrared spectrum.
3. Calculation of the Barrier To Internal Rotation In Ethane
   R. M. Pitzer and William S. Lipscomb
   J. Chem. Phys. 39, 1995 (1963)
   DOI: 10.1063/1.1734572
   One of the first theoretical calculations of the rotational barrier in ethane, from future Nobel laureate William S. Lipscomb.
4. The barrier to internal rotation in ethane
   Russell M. Pitzer
   Accounts of Chemical Research 1983 16 (6), 207-210
   DOI: 10.1021/ar00090a004
   A review on the history of determining the rotation barrier in ethane, estimated at about 2.90 kcal/mol at the time of writing (1983). Note that this is not written by the Pitzer who first reported the barrier to rotation in ethane in 1936 (K.S.) , but by his son Russell, who made important contributions to the same field in his own right.
5. Origin of rotation and inversion barriers
   Richard F. W. Bader, J. R. Cheeseman, K. E. Laidig, K. B. Wiberg, and C. Breneman
   Journal of the American Chemical Society 1990 112 (18), 6530-6536
   DOI: 10.1021/ja00174a012
   Theoretical study of the rotational barrier in ethane, methanol and methylamine, stating that the origin of the rotational barrier is not consistent with repulsion between C-H bonds! (Although they don’t mention the phrase, “hyperconjugation”, that’s what’s being implied here).
6. A notation for the study of certain stereochemical problems
   Melvin S. Newman
   Journal of Chemical Education 1955 32 (7), 344
   DOI:10.1021/ed032p344
   The original article by Newman describing his eponymous projection. Also introduces the term, “rotamers”.
7. Hyperconjugation not steric repulsion leads to the staggered structure of ethane
   Pophristic, V. ; Goodman, L.
   Nature 411, 565-568 2001
   DOI: 10.1038/35079036
   An argument that the origin of the rotational barrier in ethane is due to hyperconjugation.
8. The Case for Steric Repulsion Causing The Staggered Conformation of Ethane
   Bickelhaupt, F.M.& Baerends, E. J.
   Angew. Chem. Int. Ed. 42, 4183-4188 2003
   DOI: 10.1002/anie.200350947
   A response to the above paper.