Equilibrium and Energy Relationships

One kcal/mol is actually a lot

This article discusses the relationship between the equilibrium constant K and the difference in energy ΔG, and explores some applications of the equation towards various examples in organic chemistry.

• The difference in Gibbs energy ΔG between two species in equilibrium is related to the equilibrium constant K according to the equation

Δ G = –RT ln K

• where R is the gas constant (0.001987 kcal K^-1 mol^-1) (we will use kcal/mol here – 1 kcal/mol = 4.184 kJ/mol)
• and T is the temperature (in Kelvin)

Two species A and B that are present as a 50:50 ratio at equilibrium corresponds to an equilibrium constant  K = 1 and an energy difference  ΔG of 0 kcal/mol.

Not very exciting!

However, graphing a range of  Δ G values versus the equilibrium constant K, allows us to see that a relatively small quantity of energy (1 kcal/mol)  at room temperature (298 K) is sufficient to provide a 84:16 ratio of products to reactants. So 1 kcal/mol is actually a lot! 

Conversely, if you know the energy difference ΔG, you can calculate the equilibrium constant K through rearranging the equation to give:

K = e^(–ΔG/RT)

The article below has both discussion of these consequences and also some quizzes where you can practice doing various calculations involving K and ΔG at various temperatures.

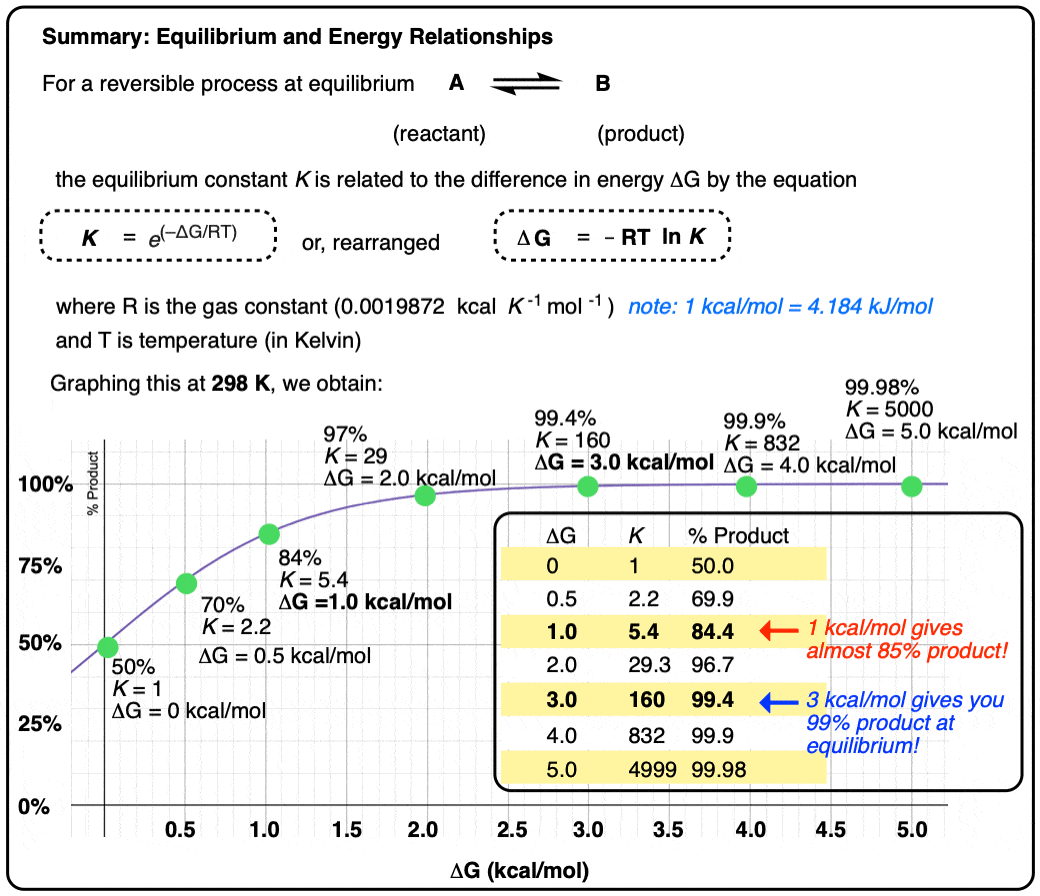
Table of Contents

1. Calculating Product Ratios For a Product At Equilibrium
2. Calculating Energy Differences (ΔG) from Equilibrium Constants
3. 1 kcal/mol Is Actually Quite A Lot
4. Calculating Equilibrium Constant K When You Have The Energy Difference (ΔG)
5. Better Selectivity “For Free” By Lowering The Temperature
6. Application – Cyclohexane “A-Values”
7. Application – Alkene Reactions
8. Application – Substitution Reaction
9. Application – Keto Enol Tautomerism
10. Summary
11. Notes
12. Quiz Yourself!
13. (Advanced) References and Further Reading

1. Calculating Product Ratios For A Reaction at Equilibrium

Let’s say we have a reversible process [Note 1] between a reactant A and a product B.

• The equilibrium constant K is equal to [ B ] / [A] where the square brackets refer to the concentrations of A and B (in mol/L) at equilibrium.
• For example, an equilibrium constant K of 5.4 means that there is a 5.4 : 1 ratio of products to starting materials at equilibrium.
• Since K is ultimately just a ratio, we can calculate the amount of product by dividing 5.4 by (5.4 + 1) to give 0.84 as the percentage composition of B, and therefore the amount of A is just whatever is left over (0.16).
• We can calculate the contribution of product B to the overall mixture by dividing the equilibrium constant K by (K + 1)

When the concentrations of A and B are equal, the equilibrium constant K is equal to 1 and the amount of B in the mixture is equal to K / (K+1) which in this case is  1 / [1+ 1] or just 0.5

Click to Flip

2. Calculating Energy Differences From Equilibrium Constants

The equilibrium constant K is related to the difference in energy Δ G between two species by the equation:

ln K = – Δ G / RT

• where R is the gas constant (0.001987 kcal K^-1 mol^-1) (Recall that 1 kcal – 4.184 kJ . We tend to use kcal/mol here because kcal units are just so darn convenient for organic chemistry [See article – Why do Organic Chemists Use Kilocalories [Note 2])
• and T is the temperature (in Kelvin)

We can now rearrange this equation to get

Δ G = –RT ln K

This means that if you can measure the equilibrium constant for a given transformation at a specific temperature, you can use it to calculate the corresponding energy difference Δ G . That’s very useful!

At room temperature (298 K), making a table of these values looks like this:

Practice doing some calculations in the quiz below.

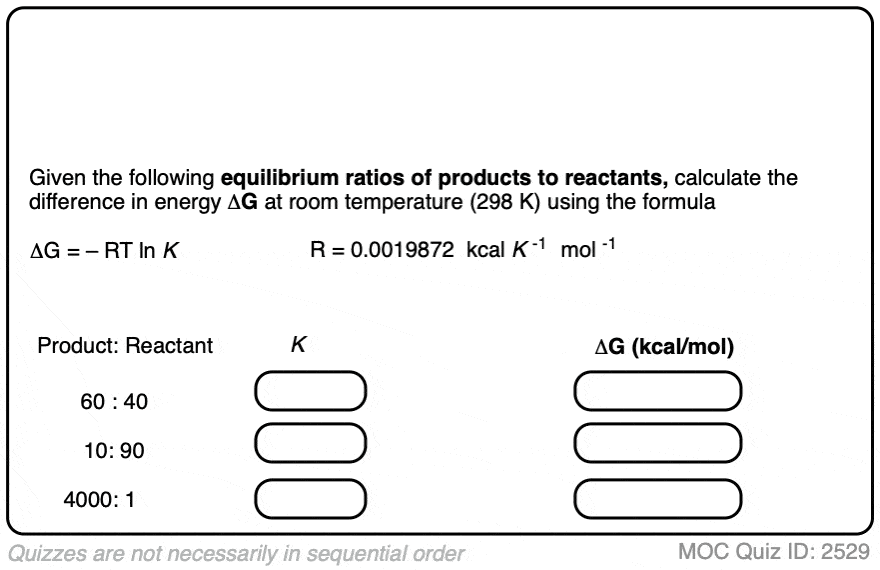Click to Flip

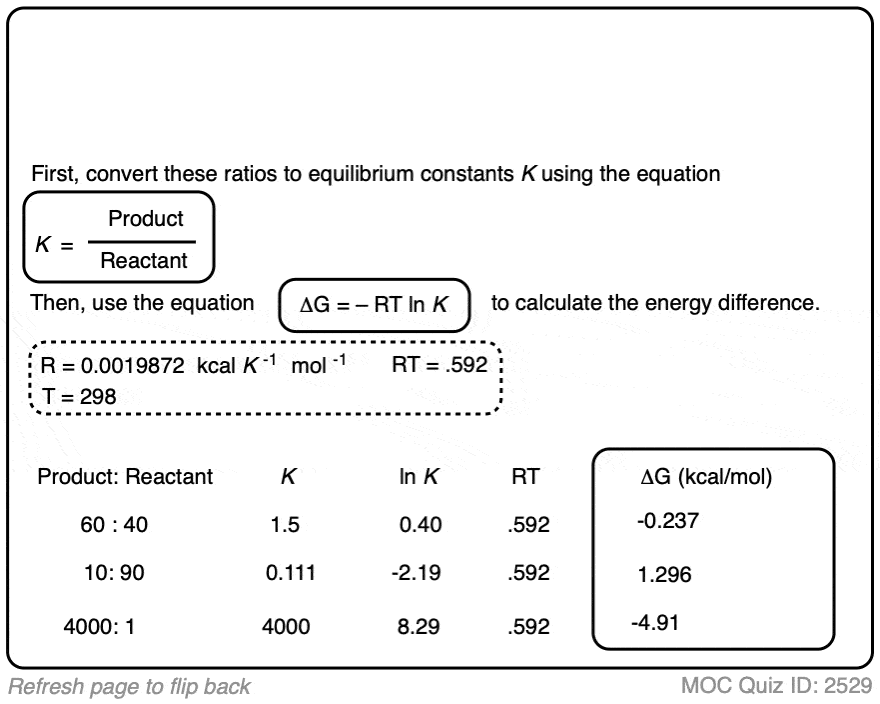
3. 1 Kcal/mol Is Actually Quite A Lot

From the table above, it’s worth pointing out that a 1 kcal/mol difference in energy gives you quite a bit of selectivity.

Graphing the product ratio versus delta G at 298 K,  gives us the following plot:

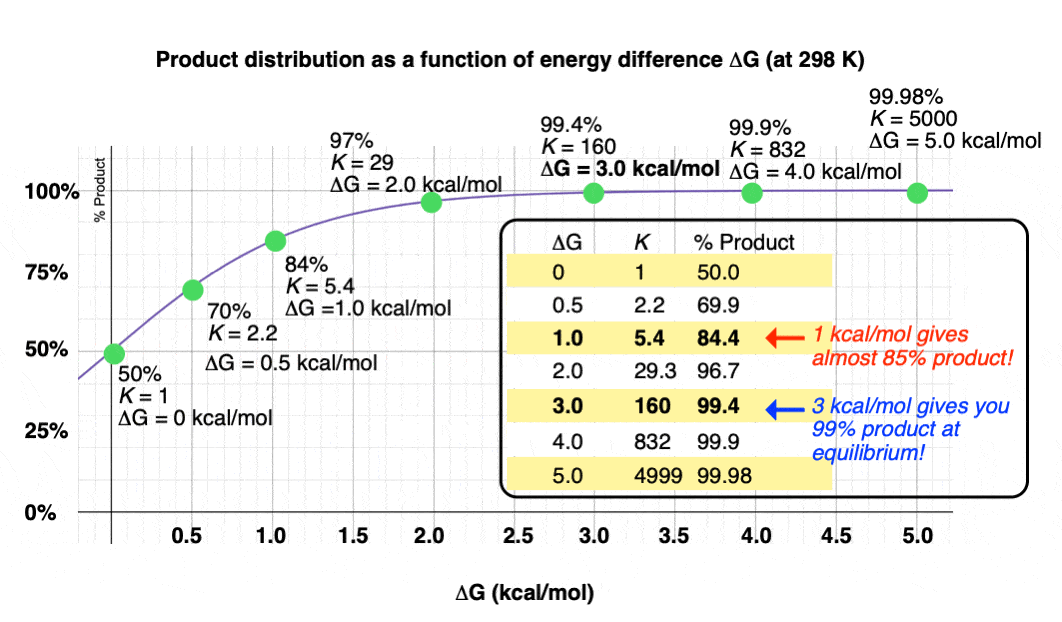
A mere 1 kcal/mol difference in energy gets you an 84:16 mixture of products. That’s pretty good selectivity for such a small energy difference.

Trust me when I say that there’s a lot of times that chemists would be happy to take an 84:16 ratio of products!

When you consider that 1 kcal/mol is just the energy cost for an H-H eclipsing interaction in ethane [See post – Staggered vs. Eclipsed Conformations in Ethane] this seems like a pretty good deal! 

If we bump up our energy difference a little bit more to 3 kcal/mol, we get over 99:1 selectivity for the product. That’s excellent.   [Note 3]

4. Calculating Equilibrium Constants From Energy Differences

We can use this equation to work in the opposite direction too.

If we know the energy difference Δ G, we can calculate the equilibrium constant K through rearranging the equation to give:

K = e^(–ΔG/RT)

When the difference in energy between two species is zero, this corresponds to an equilibrium constant K = 1

When the difference in energy is a mere 1 kcal/mol, the equilibrium constant at room temperature (298 K) is 5.4 .

This skyrockets to K = 5000 for an energy difference of 5 kcal/mol at 298 K.

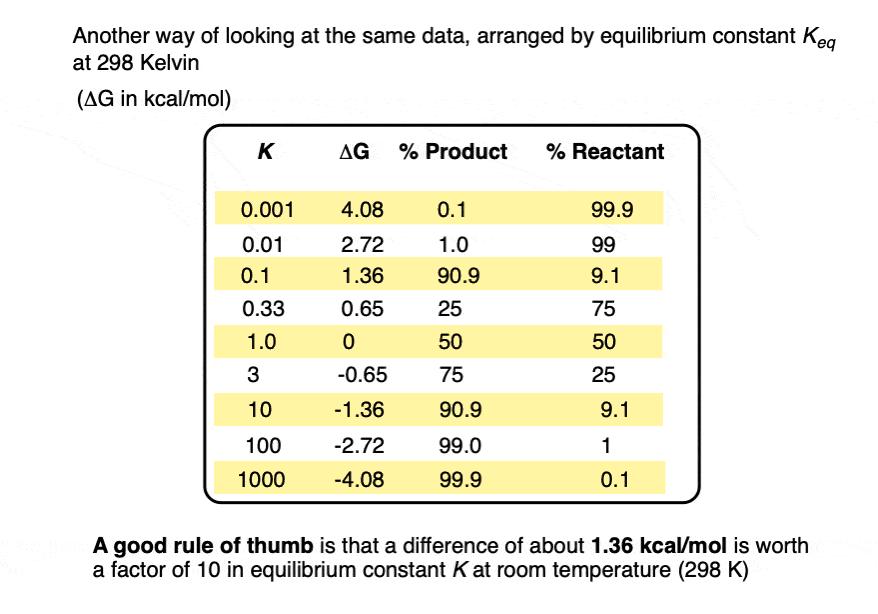
A useful rule of thumb is that each change in energy of about 1.36 kcal/mol results in an order of magnitude (10× ) increase in the equilibrium constant K. [Note 4]

Click to Flip

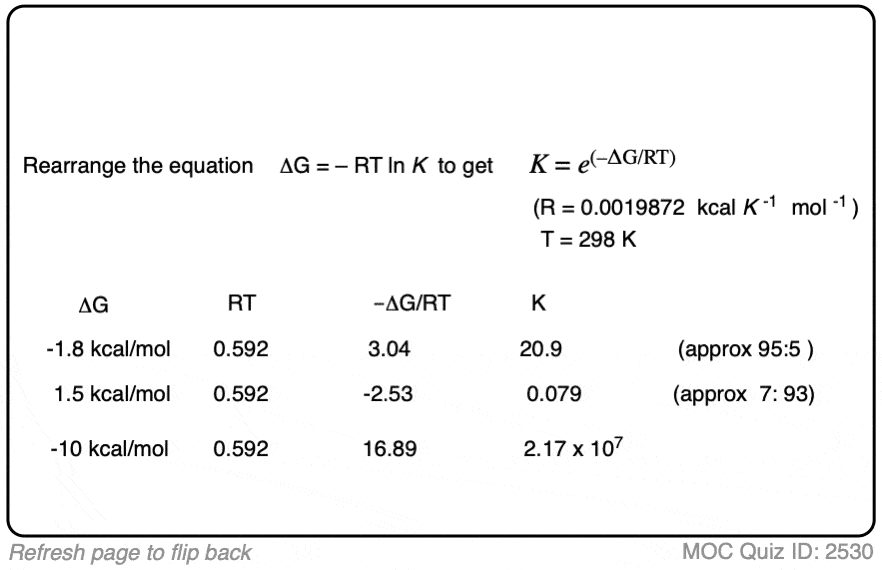
5. Better Selectivity “For Free” By Lowering The Temperature

Up until now we’ve been examining the relationship between free energy and equilibrium constant at room temperature (298 K)

What happens to the equilibrium constant when the temperature is changed?

K = e^(–ΔG/RT)

As the temperature becomes smaller,  the equilibrium constant K goes up. (assuming a spontaneous process (negative ΔG) )

In other words, for a given energy difference (e.g. 1 kcal/mol) the selectivity for the product increases.

Compare the trend in equilibrium constants for a process with ΔG 1 kcal/mol at room temperature (298 K), the freezing point of water (273 K) and the temperature of the readily available dry ice – acetone cold bath (–78°C or 195 K).

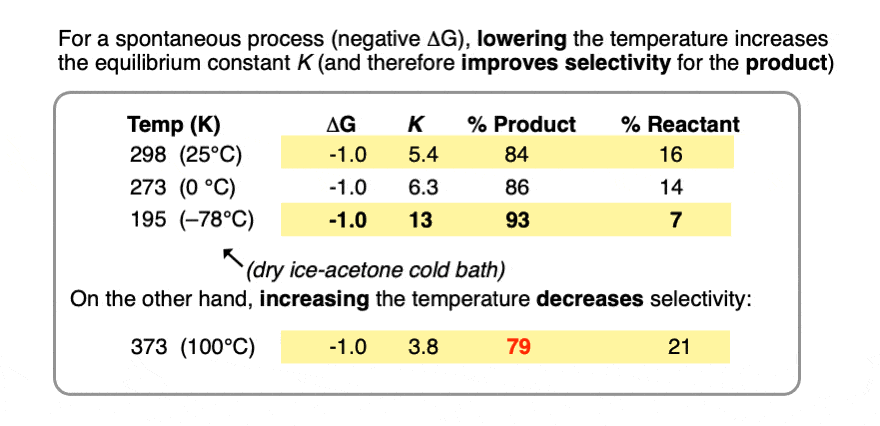
Running the reaction at extremely low temperature (-78°C) gives us an equilibrium constant K = 13 providing a 93:7 ratio of products, versus 84:16 at room temperature.

Contrast this with performing the same process at the temperature of the boiling point of water (100°C or 373 K), which gives a product ratio of 79:21 and equilibrium constant K of 3.8.

So all else being equal, if you want to maximize the selectivity of an equilibrium for a desired product, run it at the lowest temperature possible that will still give you an acceptable rate.

So what’s the catch? The last part of the previous sentence provides a clue. The price we pay for running a reaction at lower temperature is that it will be slower.

Another factor, important to note, is that running a reaction at low enough temperature might shut down the equilibrium between the two species. This is not necessarily a problem for selectivity (See article – Thermodynamic vs. Kinetic Control) but just note that using the Gibbs equation assumes the two species are in equilibrium. 

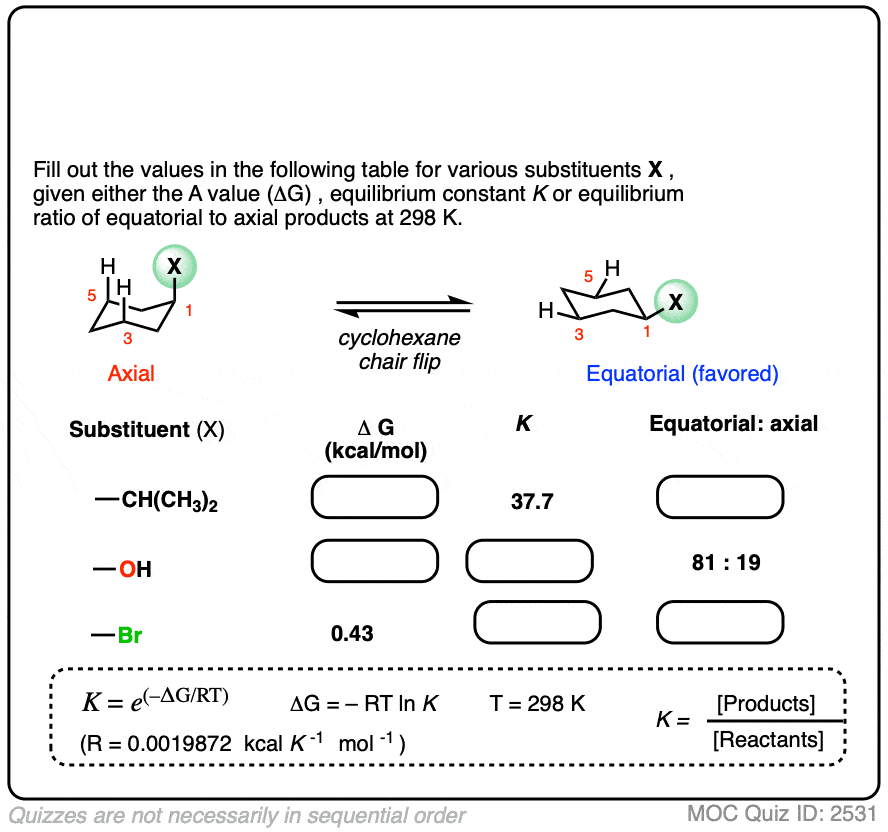
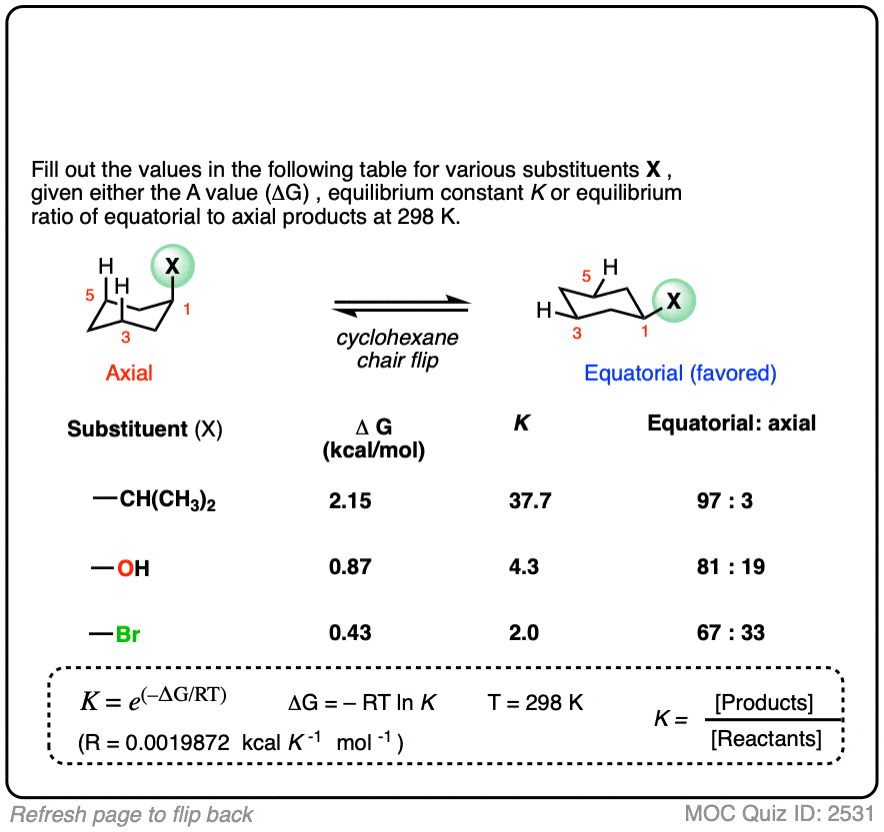
6. Application – Cyclohexane “A-values”

So if “1 kcal/mol really is a lot after all”,  this still may leave many of you with a pressing and important question:

So what?

OK, OK.  Let’s make this a bit more concrete by following up with some specific examples.

First up: cyclohexane chair flips.

Cyclohexanes adopt the “chair” conformation and interconvert between two “flipped” chair forms, where all axial substituents become equatorial and all equatorial substituents become axial. These two conformations are in equilibrium.  [See article – The Cyclohexane Chair Flip]

When a substituent is present on cyclohexane, the conformation with the substituent in the equatorial position is lower in energy than the  conformation where the substituent is axial (largely due to “gauche interactions” – steric interactions between the substituent and C-H bonds on the cyclohexane ring)

Measuring the ratio of the two conformers (NMR – Nuclear Magnetic Resonance – is a handy tool for this) allows us to calculate the equilibrium constant K, and from there we can calculate the difference in energy ΔG.

For example, at room temperature 1-methylcyclohexane exists as a 95:5 ratio of equatorial and axial conformers, which corresponds to an equilibrium constant of 17.6 and an energy difference of 1.7 kcal/mol.

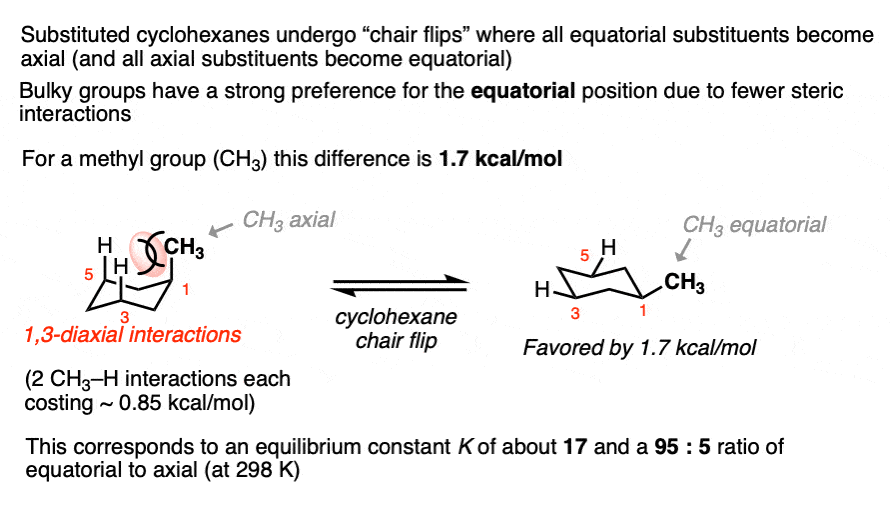
This value of 1.7 kcal/mol is often referred to as the “A-value” of the CH₃ group. (See article – Cyclohexane A-Values).

Many A-values (energy differences) for various substituents on cyclohexane have been measured and tabulated. For example, the A-value of the O–CH₃ group is 0.60 (less of a preference for the equatorial position than CH₃) and the A-value of the t-butyl group is 4.9 (extremely strong preference for the equatorial position).

In the quiz below, fill out the complete tables with the information provided:

Click to Flip

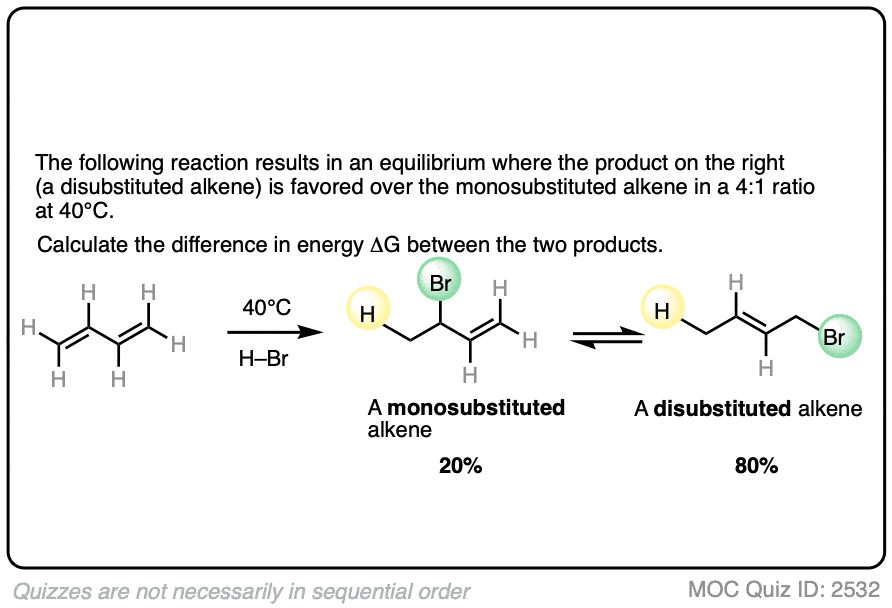
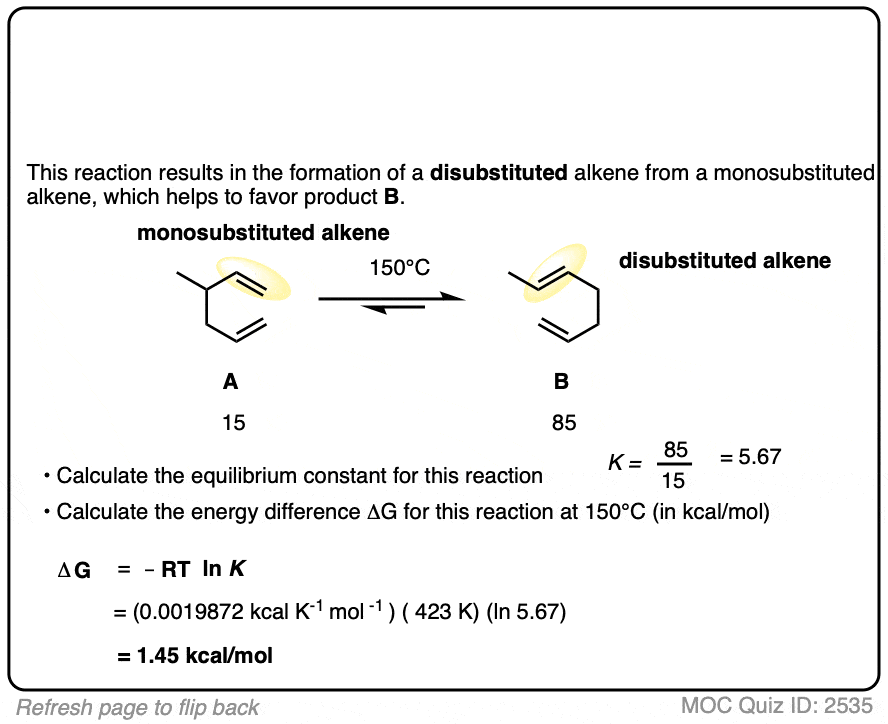
7. Application – Alkene Reactions

Here’s another example which comes up near the beginning of organic chemistry 2 for most students.

The specific details of the reaction aren’t that important for our purposes (it’s the addition of HBr to 1,3-butadiene. More details in this post on 1,2- and 1,4-additions to dienes.)

What is important is that the reaction results in an equilibrium where the two products are formed in about a 4:1 ratio favoring the disubstituted alkene over the monosubstituted alkene.

Using this information, you should be able to calculate the difference in energy (ΔG) between the two products when this reaction is performed at 40°C.

Click to Flip

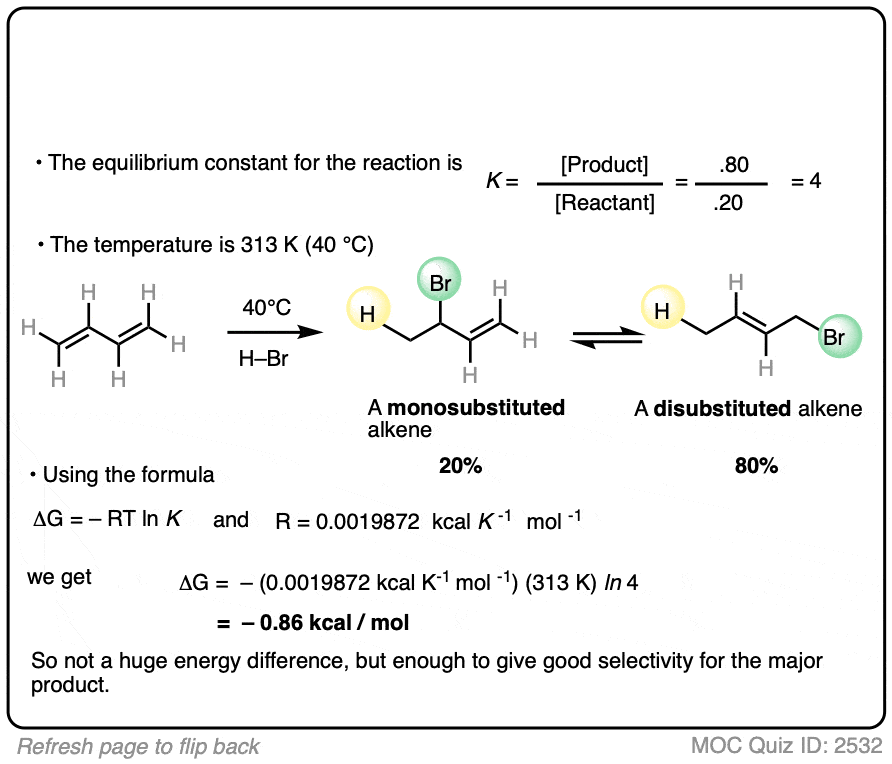
You might have already learned that alkene stability increases with substitution,  which is the basis of Zaitsev’s rule for elimination reactions. (See article – Zaitsev’s Rule).  This is not an elimination reaction, but shows the same principle at work: the more substituted alkene is more favored.

Interestingly, the difference in energy between the monosubstituted and disubstituted alkenes is not all that large [See article: Stability of Alkenes] but as this example illustrates, can lead to pretty good selectivity for the major product.

Zaitsev’s rule is ultimately based on energy differences of only about 1 kcal/mol or so! 

8. Application – Substitution Reactions

We can also apply these relationships to substitution reactions.

A substitution reaction, for our purposes, is one where a bond is formed and broken on the same carbon. In contrast to acid-base reactions, which are generally drawn as equilibria, substitution reactions tend to be irreversible. [Note 5]

For many practical nucleophilic substitution reactions of alkyl halides, the difference in energy ΔG has been calculated to be between 10 and 20 kcal/mol. [Ref]

(This reflects both the greater bond strengths of C-O, C-N, or C-C bonds relative to C-Cl, C-Br, or C-I bonds as well as the much lower basicity of the Cl(-), Br(-), or I(-) leaving group relative to that of most nucleophiles). 

Using one of these experimentally determined differences in energy to calculate the equilibrium constant K is a useful exercise.

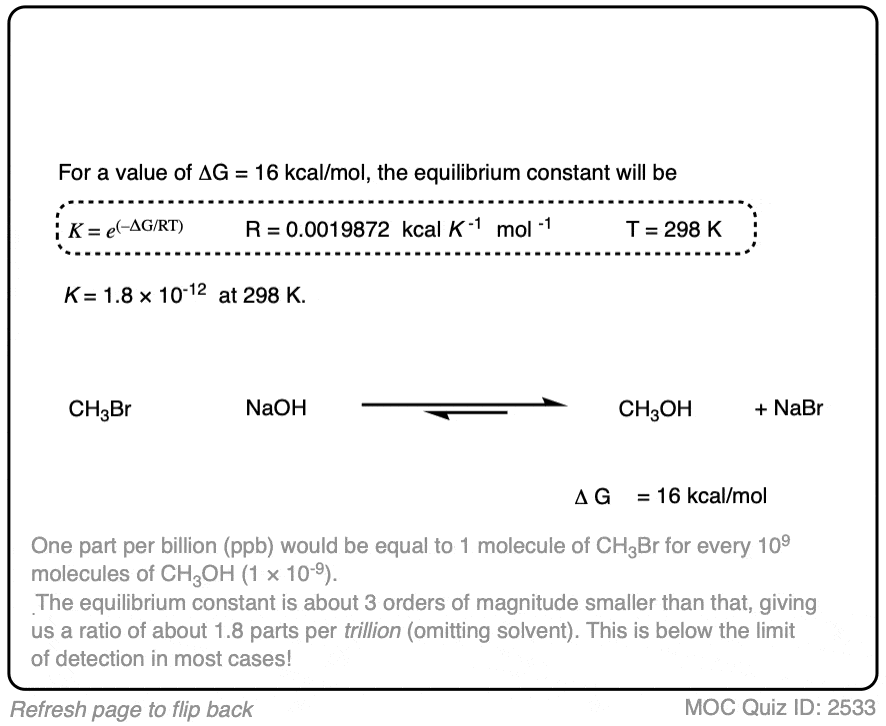
In the exercise below, calculate the equilibrium constant of the reaction between NaOH and CH₃Br at 298K given that the difference in energy is about 16 kcal/mol. [REF]

Click to Flip

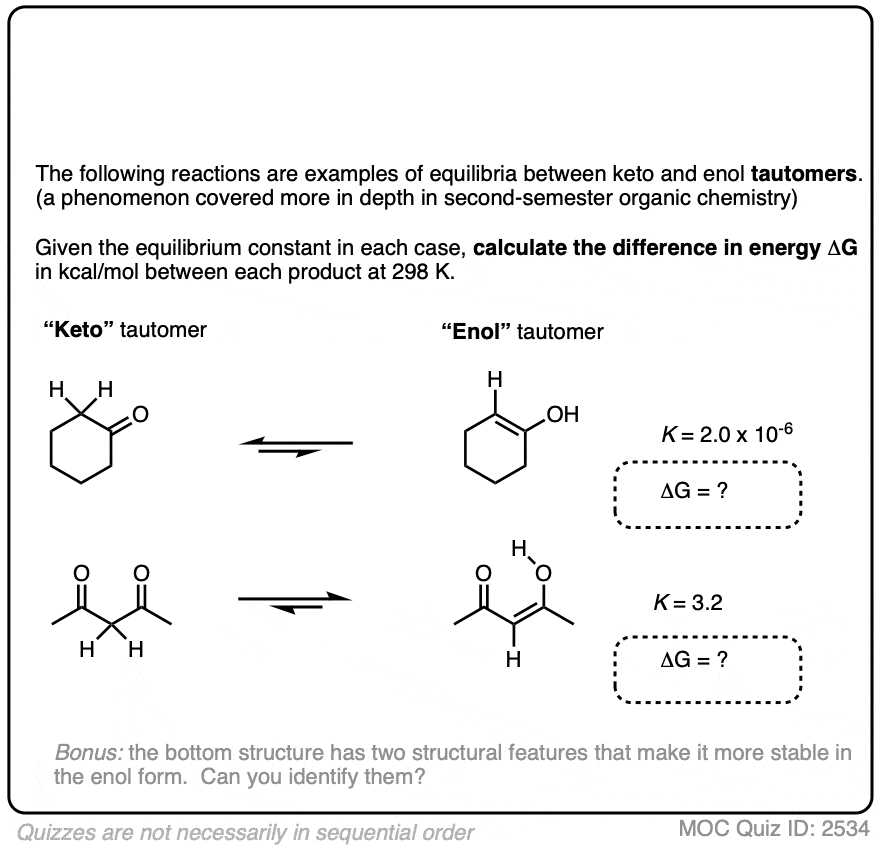
9. Application – Keto-Enol Tautomerism

We’re kind of going on a grand tour of sophomore organic chemistry using this concept. Anyway, here’s another example of applying the relationship between equilibrium constants and energy differences.

Aldehydes and ketones are known to be in equilibrium with a structural isomer known as their enol form. This process is known as keto-enol tautomerism. (For more information, see this article – Keto Enol Tautomerism).  The details of this reaction don’t concern us for the purposes of this post, as we are really only going to focus on equilibrium constants and energy differences.

The ratio of keto:enol depends on many factors, mostly having to do with the structure of the carbonyl compound, although solvent can also play a significant role.

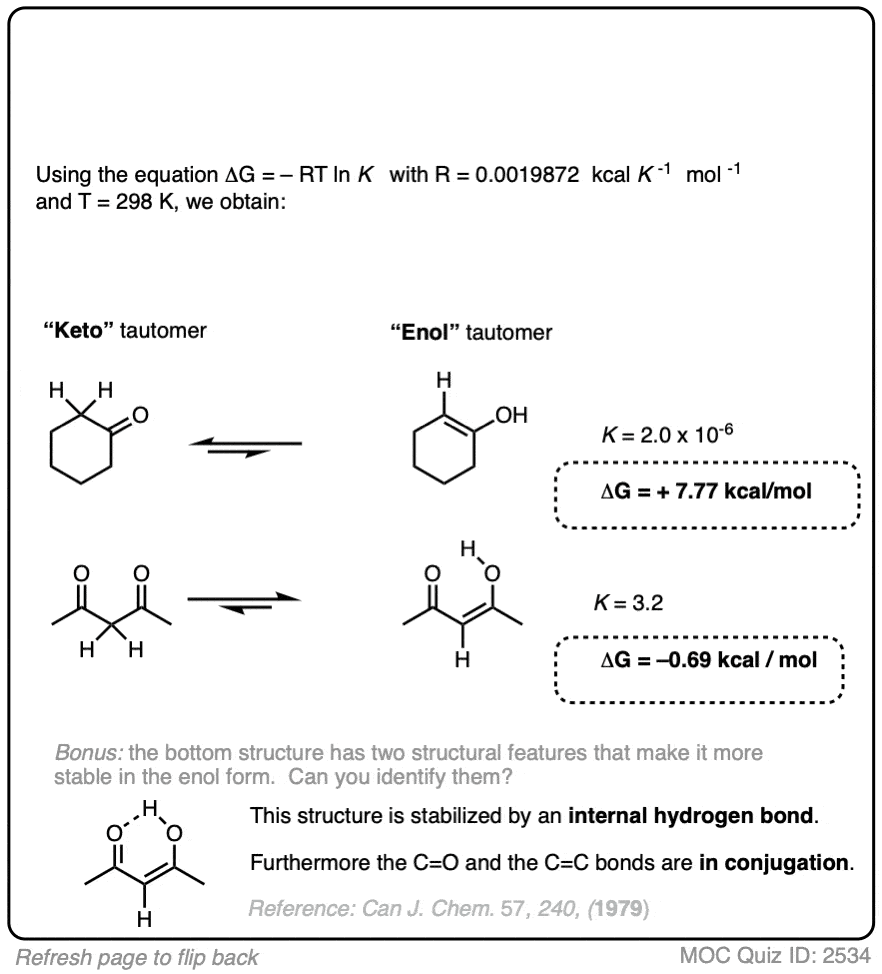
For most aldehydes and ketones, the equilibrium strongly favors the keto form. For example, for cyclohexanone, the equilibrium constant K for formation of the enol is 2.0 × 10^–6  . So every molecule of the enol  is outnumbered by the keto by a factor of about a million to one.

We can use the equilibrium constant, combined with the temperature T to calculate the difference in energy ΔG between the keto and enol forms.

Try the two examples in the exercise below:

Click to Flip

10. Summary

Before we go, I should stress that just because a product isn’t favored by equilibrium doesn’t necessarily make it unimportant. There are many cases of reactions where a product is formed through an unfavorable equilibrium, but, once formed, that product is highly reactive in a subsequent reaction, and eventually the entire starting material is consumed.  (A classic example is deprotonation of esters by alkoxides in the Claisen condensation – see article. Note 6).

So let’s summarize the key points.

• The equilibrium constant K between two species is related to their difference in energy ΔG. Knowing one value allows you to calculate the other.
• An energy difference of 1 kcal/mol doesn’t sound like very much, but is enough to produce an 84:16 ratio of products at room temperature. A difference in energy of 3 kcal/mol is enough to produce a 99:1 ratio.
• At lower temperatures, the equilibrium constant increases (giving greater selectivity).
• Higher temperatures reduce selectivity.
• The relationship between equilibrium constant and ΔG can be applied in numerous ways throughout introductory organic chemistry, including (but not limited to) substituted cyclohexanes (A-values), addition to alkenes, nucleophilic substitution reactions, and keto-enol tautomerism.

Notes

Note 1. I say “process” here so as to include both reactions and also phenomena like conformational changes (e.g. cyclohexane chair flips). “Process” is a good vague word that covers all the bases.

Note 2. Why use kilocalories? It just happens to be very convenient for organic chemistry because a lot of chemical phenomena occur within the range from 1-100 kcal/mol, which makes values much easier to remember.

For example, a value of 100 kcal/mol corresponds to one of the stronger bond dissociation energies for a single bond, the C-H bond dissociation energy in ethane.

A value of 1 kcal/mol corresponds to one of the lowest-energy interactions organic chemists routinely consider,  the torsional strain of two eclipsed C-H bonds in ethane. [See article: Staggered vs. Eclipsed Conformations of Ethane]

So on one end of the scale, you’ve got a very high-energy process (C-H bond breaking) and on the other, a very low-energy interaction (H-H repulsion), and a ton of other phenomena in between.

It’s just easier, mentally, to use a 1-100 scale than it is to use a 4.184 to 418.4 scale. That might not be the case in other fields of chemistry, but in organic chemistry, kcal/mol is convenient.  Take that, metric system!

Note 3. Once you get to a 99:1 of products  it starts to become difficult to accurately measure the amount of minor products due to the fact that our most of the techniques used for determining product ratios involve determining the area under peaks in NMR (nuclear magnetic resonance) spectra or HPLC (high-pressure liquid chromatography) chromatograms and the area under the minor peaks starts to become difficult to discern from baseline noise.

So if “1 kcal/mol is a lot”, it’s fair to say that “3 kcal/mol is enough” for establishing a selective process.

Note 4. This relationship is explicitly mentioned in the excellent textbook “Modern Physical Organic Chemistry” by Anslyn and Dougherty. Highly recommended for upper year organic chemistry majors and graduate students.

Note 5. Nucleophilic substitution reactions are more often found to be reversible when both the nucleophile and leaving group are both very weak bases and have similar pK_a values. Substitution reactions between alkyl halides with halide ions are one example (e.g. CH₃CH₂Br + NaI –> CH₃CH₂I + NaBr) .

Note 6. In the Claisen condensation the acid-base reaction is disfavored by about 8 pK_a units and still works well. There are limits, however. A decent rule of thumb (from Grossman’s Art of Writing Reasonable Reaction Mechanisms) is to treat reactions with equilibrium constants of 10¹⁰ or more as being essentially irreversible.

Quiz Yourself!

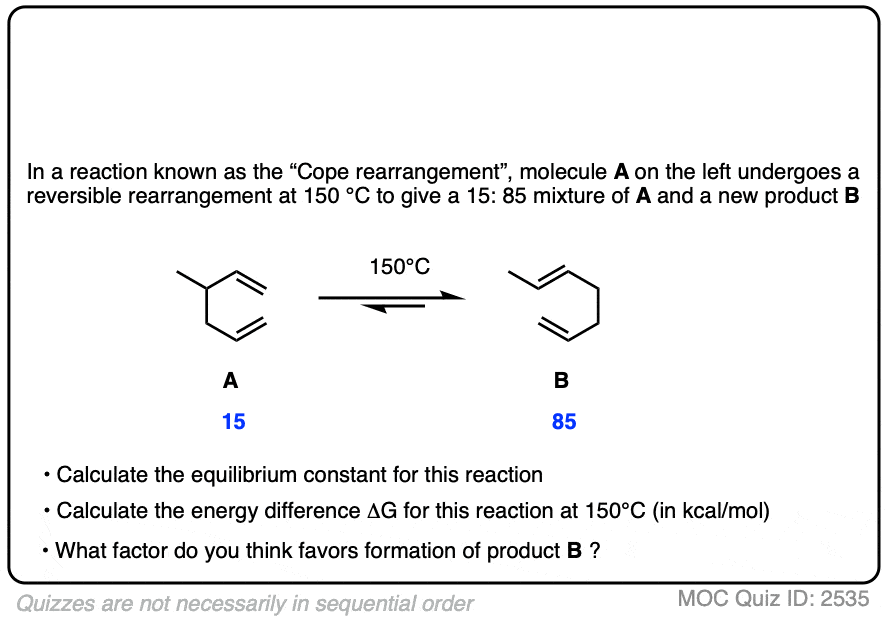Click to Flip

(Advanced) References and Further Reading

References

1. Neighboring Carbon and Hydrogen. XIX. t-Butylcyclohexyl Derivatives. Quantitative Conformational Analysis
   S. Winstein and N. J. Holness
   Journal of the American Chemical Society 1955 77 (21), 5562-5578
   DOI: 10.1021/ja01626a037
   A key paper introducing the concept of “A-values”, in particular a study on t-butyl substituted cyclohexanes.

2. Mechanism of ionic reactions. The heat of ionic substitution reactions
   R. A. Ogg
   Trans. Faraday Soc., 1935,31, 1385-1392
   DOI: 10.1039/TF9353101385
   Study on the thermodynamics of substitution reactions, finding that the reactions of alkyl halides with ethoxide, phenoxide, acetate, hydrosulfide, cyanide, thiosulfate and sulfite ions are all exothermic by 10-20 kcal/mol.