Aromaticity
Rules For Aromaticity
Last updated: February 5th, 2025 |
Rules For Aromaticity: The 4 Key Factors
In the last post we introduced the concept of aromaticity, a property of some unusually stable organic molecules such as benzene. Although some aromatic molecules are indeed fragrant (hello, vanillin! ) the term “aromaticity” actually has nothing to do with smell. We saw that aromatic molecules:
- have an extremely high resonance energy (36 kcal/mol for benzene)
- undergo substitution rather than addition reactions
- have delocalized pi-electrons
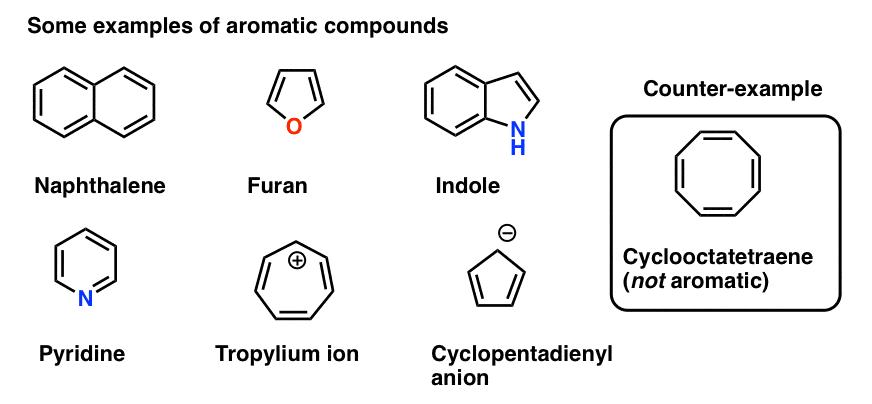
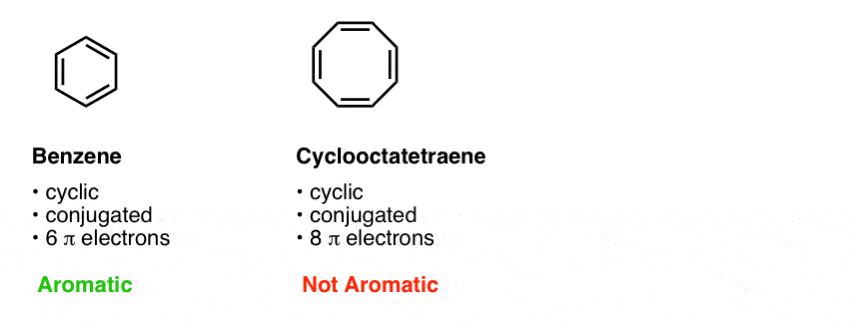
We also gave a few example of other molecules besides benzene which are aromatic, and some which look similar to benzene (e.g. cyclooctatetraene) which are not.
So what are the rules? How can we predict whether a molecule is aromatic or not?
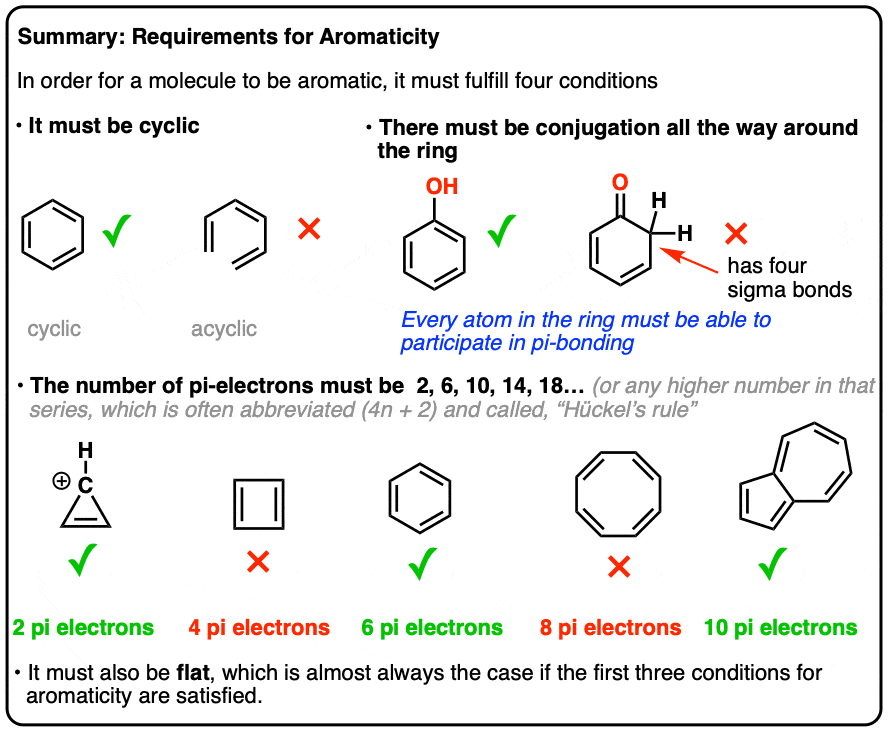
Table of Contents
- Four Key Rules for Aromaticity
- Condition #1 for Aromaticity: The Molecule Must Be Cyclic
- Condition #2: Every atom in the ring must be conjugated
- Condition #3: The Molecule Must Have [4n+2] Pi Electrons
- Which Electrons Count As “Pi Electrons”?
- Pyridine and the Benzene Anion
- Some Examples With 5-Membered Rings
- Condition #4: The Molecule Must Be Flat
- Summary: Rules For Aromaticity
- Notes
- Quiz Yourself!
- (Advanced) References and Further Reading
1. Four Key Rules For Aromaticity
There turn out to be 4 conditions a molecule must meet in order for it to be aromatic.
It’s all or nothing. If any of these conditions are violated, no aromaticity is possible.
- First, it must be cyclic.
- Second, every atom in the ring must be conjugated.
- Third, the molecule must have [4n+2] pi electrons (we’ll explain in depth what that means, below)
- Fourth, the molecule must be flat (usually true if conditions 1-3 are met, but there are rare exceptions)
Let’s go into more detail.
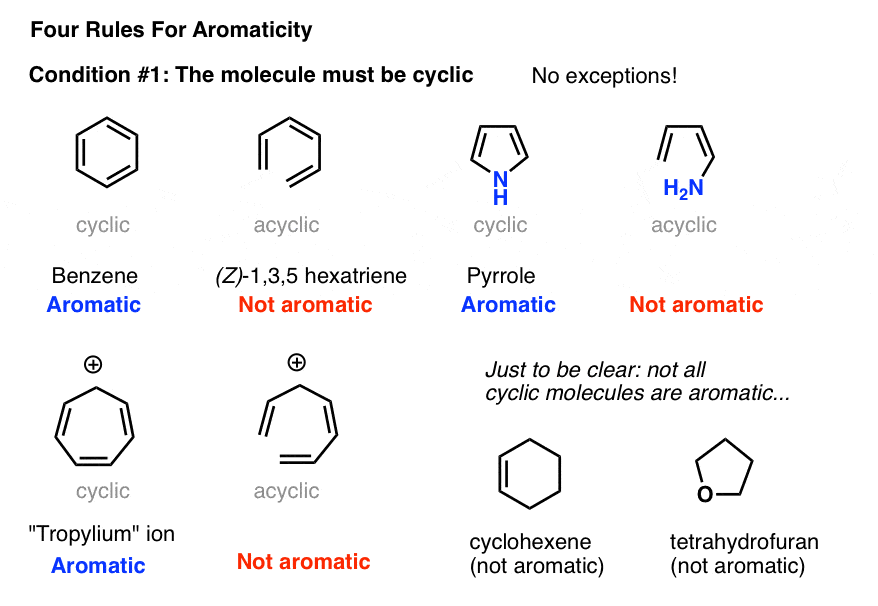
2. Condition #1 for Aromaticity: The Molecule Must Be Cyclic
Determining if a molecule is cyclic is pretty straightforward. Is there a ring? If yes, move to condition #2. If there’s no ring, forget it.
Case in point: (Z)-1,3,5 hexatriene has the same number of pi bonds (and pi electrons) as benzene, but isn’t aromatic. No ring, no aromaticity.
3. Condition #2 For Aromaticity: Every Atom In The Ring Must Be Conjugated
Obviously, being cyclic isn’t a sufficient condition for aromaticity. Just look at cyclohexene, above right. Not aromatic.
In order for aromaticty to exist, there must also be a continuous ring of p-orbitals around the ring that build up into a larger cyclic “pi system”.
One way of saying this is that every atom around the ring must be capable of conjugation with each other .
There are a few alternative ways to say the same thing.
We can also say:
- “Every atom in the ring must have an available p orbital”, or
- “Every atom in the ring must be able to participate in resonance”.
Remember that the “available p orbital” condition applies not just to atoms that are part of a pi bond, but also atoms bearing a lone pair, a radical, or an empty p orbital (e.g. carbocations). [See this post on conjugation and resonance if you are unsure].
The key thing that “kills” conjugation is an sp3 hybridized atom with four bonds to atoms. Such an atom cannot participate in resonance.
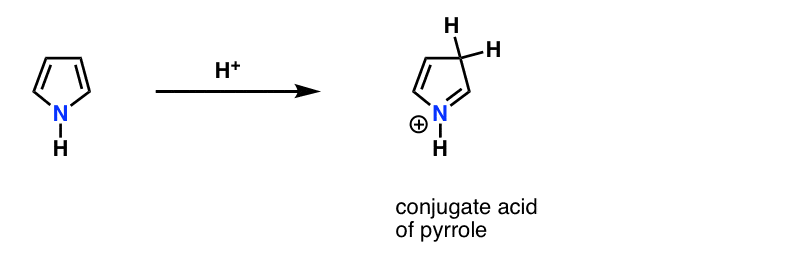
This is why the lone pair on pyrrole (below) isn’t as basic as you’d expect a nitrogen to be. Protonation of the nitrogen disrupts the conjugation around the ring, destroying aromaticity in the process. [Note 1]
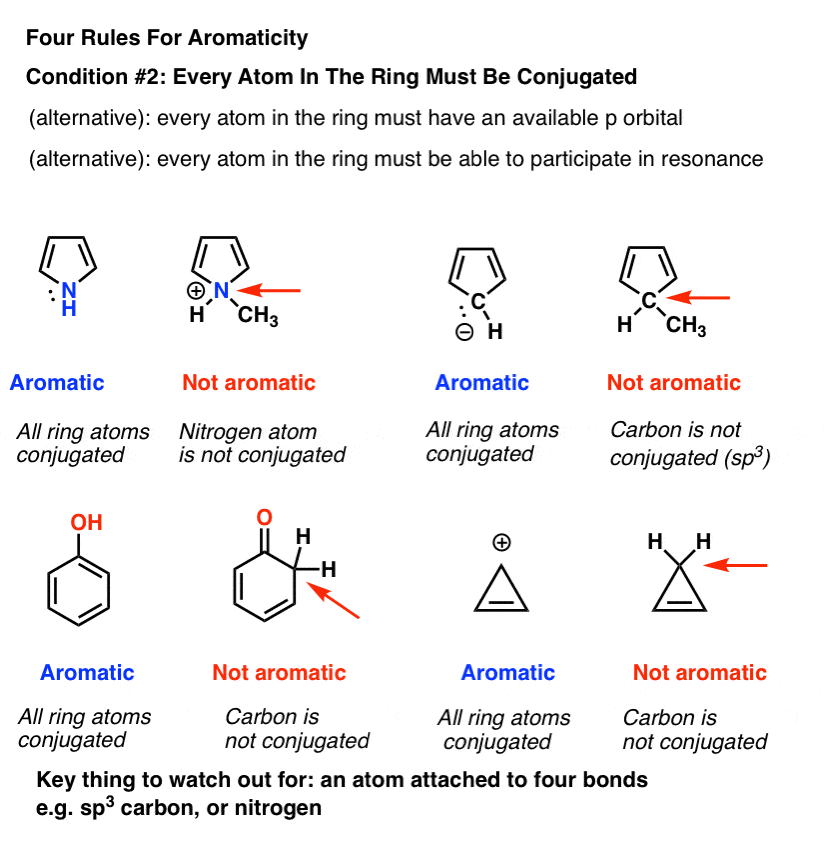
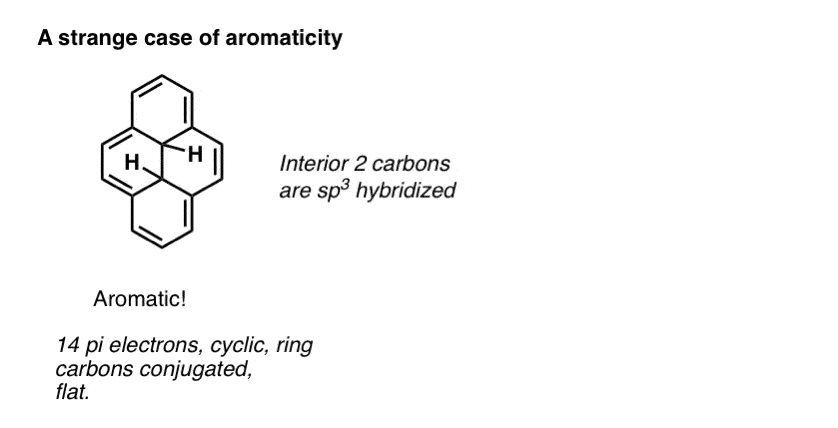
Advanced note. There’s actually several molecules which are conjugated around the perimeter of the ring but the interior carbons are sp3 hybridized. Still counts as aromatic. [Note 2]
4. Condition #3 For Aromaticity: The Molecule Must Have [4n+2] Pi Electrons
The third condition is that the cyclic, conjugated molecule must have the correct number of pi electrons. Benzene and cyclooctatetraene are both cyclic and conjugated, but benzene is aromatic and cyclooctatetraene is not. The difference is that benzene has 6 pi electrons, and cyclooctatetraene has 8. [We’ll explain why this makes a difference in subsequent posts].
Our quick shorthand we often use is to say that benzene has [4n+2] pi electrons and cyclooctatetraene does not.
However, this term [4n+2] causes a lot of confusion in organic chemistry. I’ve known students who will stare at a molecule and try to figure out what “n” is.
“n” is not a property of the molecule!
Commenter Claire had a great way of putting it:
“4n+2 is not a formula that you apply to see if your molecule is aromatic. It is a formula that tells you what numbers are in the magic series. If your pi electron value matches any number in this series then you have the capacity for aromaticity.”
Exactly! The “magic series” is: 2, 6, 10, 14, 18, 22….. (and counting up from 4 after that). [Note 3]
[4n+2] is mathematical shorthand for writing out the series [2, 6, 10, 14, 18, 22…] .
We can generate this series by plugging in whole numbers (“n” = 0, 1, 2, 3, 4… ) to the [4n+2] formula. Those values of “n” have nothing to do with molecules. We are just using them to generate the series.
So for n = 0 , we have [4 (0) + 2] = 2
for n = 1 , we have [4 (1) + 2 ] = 6
for n = 2, we have [4 (2) + 2 ] = 10
for n = 3, we have [4 (3) +2 ] = 14
And so on. See how it generates the series [2, 6, 10, 14…] ? That’s the point of [4n+2].
The numbers in this “magic series” are sometimes referred to as “Hückel Numbers” after Erich Hückel, who proposed this rule back in 1931.
The condition that aromatic molecules must have [4n+2] pi electrons is sometimes called “Hückel’s rule”.
In the figure below, molecules which fulfill Hückel’s rule are in green; those which do not fulfill Hückel’s rule are in red.
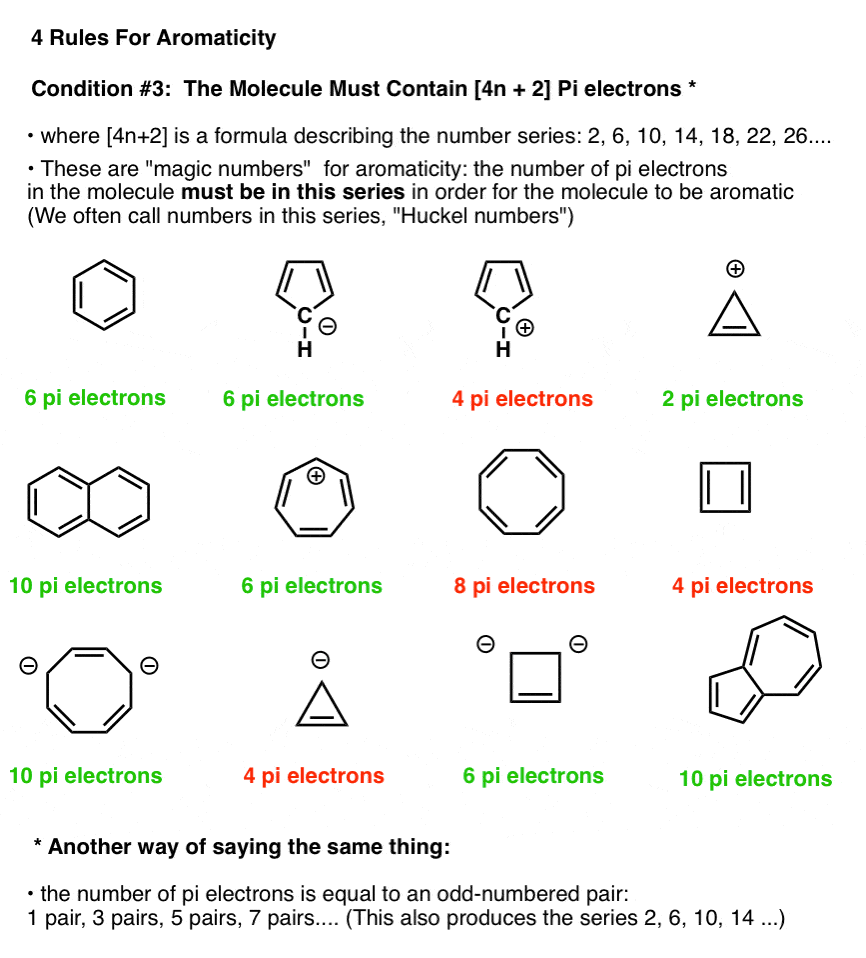
Note that we can count electrons in pi bonds as well as electrons from lone pairs (so long as the carbon isn’t already participating in a pi bond – see below). So the cyclopentadiene anion has six pi electrons – 4 from the two double bonds, and two from the lone pair on carbon.
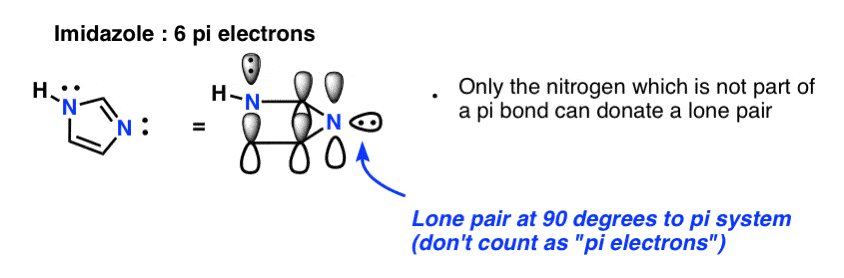
5. Which Electrons Count As “Pi Electrons”, And Which Do Not?
That seems straightforward enough. However, complications can arise when we have atoms in the ring which both participate in pi bonding and also have a lone pair. For example,
- how do we count electrons in the benzene anion (below left) or pyridine? Do we count the lone pair electrons as Pi electrons, giving a total of 8? Or do we ignore them?
- What about furan (middle) which has two lone pairs on oxygen?
- What about pyrrole, with its lone pair on nitrogen, or imidazole, with two nitrogens?
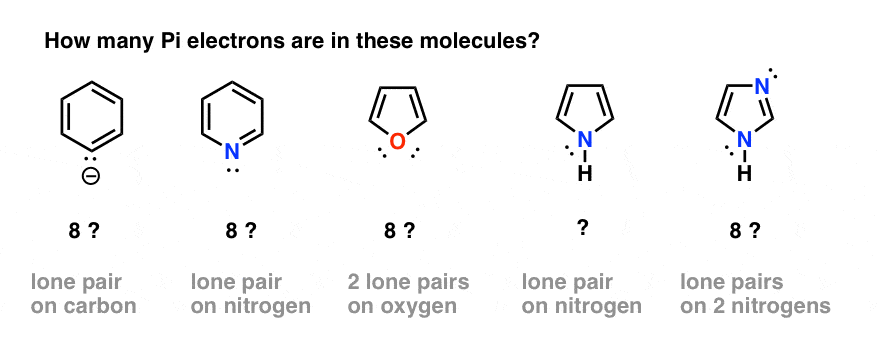
In order to answer these questions, it’s important to remind ourselves of how p orbitals contribute to aromaticity in benzene.
In benzene, each p orbital is arranged at right angles (90°) to the plane of the ring. Each p orbital contains a single electron. We can verify the total number of pi electrons in benzene by counting the pi bonds: 3 pi bonds times two electrons = 6 pi electrons total.
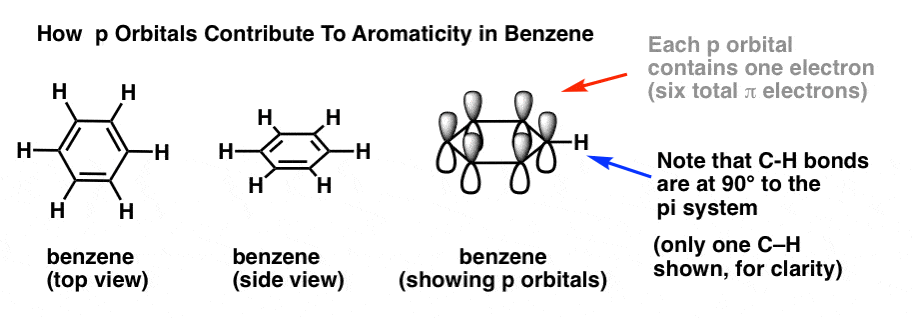
Note that the C-H bonds are at 90° to the pi system. If there was a lone pair where the C-H bond is, then it wouldn’t be able to interact with the pi system at all. Which brings us to….
6. Some Electrons Don’t Count: Pyridine and the Benzene Anion
The benzene anion has a lone pair on one of the carbons. This lone pair can’t be in a p orbital, since the p-orbital is participating in the pi system. Instead, it’s at 90 degrees to the pi system, in the plane of the ring.
In other words, the lone pair on carbon doesn’t count as a pair of pi electrons since it can’t overlap with the pi system.
The same is also true for pyridine, where the lone pair is also at right angles to the pi system.
So while in each case you might be tempted to say that they have 8 pi electrons, the correct answer is 6. This is a Hückel number, and both of these molecules are in fact aromatic.

The bottom line: each ring atom can contribute a maximum of one p orbital toward the pi system.
7. Some Examples Of Aromatic 5-Membered Rings
Some molecules with five-membered rings can also present ambiguities.
The cyclopentadiene anion (below) has a lone pair on one of the carbons. Can this lone pair contribute to the pi system?
Since that carbon is not involved in any pi-bonding, the answer is yes.
The total number of pi electrons for the cyclopentadiene anion equals 2 (from the lone pair) plus the 4 electrons in the two pi bonds, giving us a total of 6. This is a Hückel number and the cyclopentadiene anion is in fact aromatic.

A similar situation arises for pyrrole. The nitrogen bears a lone pair but is not involved in a pi bond (unlike pyridine, above). Therefore it can contribute to the pi system and this gives us a total of 6 pi electrons once we account for the 4 electrons from the two pi bonds.

A curious case is furan, where the oxygen bears two lone pairs. Does this mean that furan has 8 pi electrons? No!
Why not? Because as we noted above, each atom can contribute a maximum of one p-orbital towards the pi system. In furan, one lone pair is in a p orbital, contributing to the pi system; the other is in the plane of the ring. This gives us a total of 6 pi electrons. Furan is aromatic. (So is thiophene, the sulfur analog of furan).

Finally there is imidazole, which has two nitrogens. One nitrogen (the N-H) is not involved in a pi bond, and thus can contribute a full lone pair; the other is involved in a pi bond, and the lone pair is in the plane of the ring. This also gives us a total of 6 pi electrons once we account for the two pi bonds.
8. Condition #4 For Aromaticity: The Molecule Must Be Flat
The fourth condition for aromaticity is that the molecule must be flat (planar).
Aromaticity is such a stabilizing property (worth 20-36 kcal/mol) that generally a molecule that is
- cyclic
- conjugated
- has [4n+2] pi electrons
will also be flat. Give a molecule a large enough potential energy well, and it will fall into it eventually.
It’s a bit like the punch line to the old (crude) joke about why dogs adopt a certain energetically favourable conformation: “Because they can”.
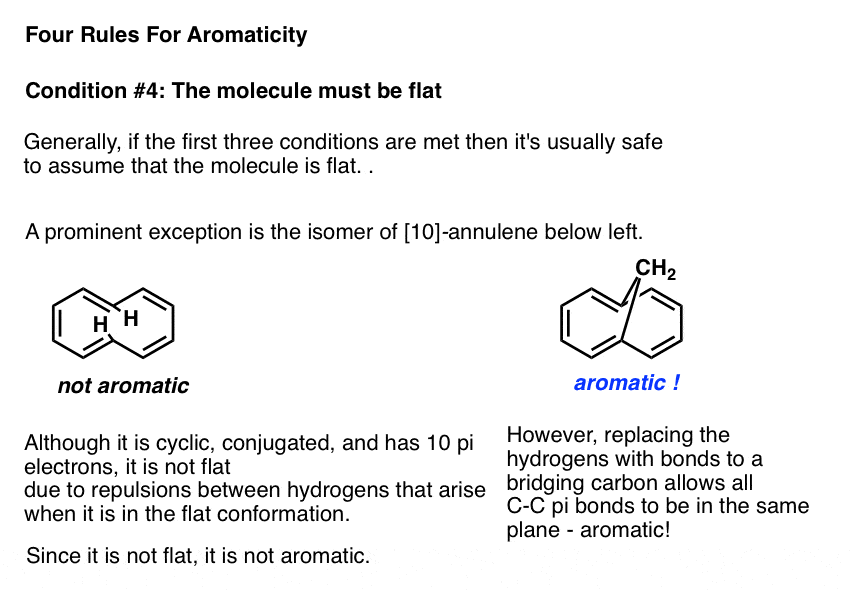
As with certain vertebrates, the only thing that preventing a molecule that fulfills the first three conditions from being flat is if the flat conformation is incredibly strained. One example in this category is the molecule known as [10]-annulene, an isomer of which is drawn below left. In the trans, cis, trans, cis, cis isomer, the molecule is cyclic, conjugated, and has 10 pi electrons, but the two marked hydrogens bump into one another when attempting to adopt a flat conformation.
The molecule is prevented from adopting planarity due to this punitive Van Der Waals strain , and is therefore not aromatic.
Interestingly, if the hydrogens are removed and replaced with a bridging CH2 group, the strain is relieved and the pi bonds can adopt a planar conformation. The molecule below right shows the expected properties of an aromatic molecule.
9. Summary: Rules For Aromaticity
This post went through the four conditions a molecule must meet to be aromatic.
Generally, determining if a molecule is cyclic and conjugated isn’t what trips people up.
It’s the damn pi electron-counting!
So in the next post, we’ll play the game show “Is This Aromatic?” with a series of different contestants and try to demonstrate a relatively quick n’ easy plan for determining if an unknown molecule is aromatic or not.
After that, we’ll look at the molecular orbitals and attempt to understand what exactly is so special about the Hückel series.
Thanks to Matt Knowe for assistance with this post.
Check out these worked examples
Notes
 Click to Flip
Click to Flip

Note 1. Fun fact. Pyrrole actually reacts with acid on carbon, not nitrogen!
Note 2. Weird case: the one with aromaticity around the exterior but not on the inside.
Note 3. It should be noted that Huckel’s rule starts to break down for higher numbers of pi electrons (>20) in polycyclic systems. I’m not going to go into the details here. The wikipedia article covers it well.
Quiz Yourself!
 Click to Flip
Click to Flip


Become a MOC member to see the clickable quiz with answers on the back.

Become a MOC member to see the clickable quiz with answers on the back.

Become a MOC member to see the clickable quiz with answers on the back.

Become a MOC member to see the clickable quiz with answers on the back.

Become a MOC member to see the clickable quiz with answers on the back.
(Advanced) References and Further Reading
- Quantentheoretische Beiträge zum Benzolproblem
Die Elektronenkonfiguration des Benzols und verwandter Verbindungen
Erich Hückel
Zeitschrift für Physik 1931, 70, 204–286
DOI: 10.1007/BF01339530
Erich Hückel achieved recognition by elaborating, together with Peter Debye, the theory of strong electrolytes in 1923 and later by applying a simplified version of quantum theory to p-electrons in conjugated molecules, which became known as Hückel molecular orbital (HMO) theory. Although he never explicitly formulated a “4n + 2 rule”, this was obvious from his work. Hückel showed that monocyclic systems with continuous conjugation having 6, 10, 14, etc. p-electrons benefited from extra stabilization and were aromatic. But it is more accurate to refer to the “Hückel 4n + 2 p-electron rule,” rather than to “Hückel’s rule.” - Aromaticity Today: Energetic and Structural Criteria
Mikhail Glukhovtsev
Journal of Chemical Education 1997, 74 (1), 132
DOI: 1021/ed074p132
This paper discusses two of the criteria for establishing aromaticity – planarity and a positive stabilization energy. The latter can be verified by computational methods, as the article demonstrates. - Global aromaticity at the nanoscale
Rickhaus, M., Jirasek, M., Tejerina, L. et al.
Nature Chem. 12, 236–241 (2020)
DOI: 10.1038/s41557-019-0398-3
This paper was published in early 2020 and officially sets the record for the largest aromatic system, with 162 p electrons! Evidence for aromaticity comes from both NMR measurements and experimental (NICS) calculations. - Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe
Paul von Ragué Schleyer, Christoph Maerker, Alk Dransfeld, Haijun Jiao, and Nicolaas J. R. van Eikema Hommes
Journal of the American Chemical Society 1996, 118 (26), 6317-6318
DOI: 10.1021/ja960582d
This paper is an advanced topic but worth including here, as it is one of Prof. Schleyer’s most highly cited papers. Aromaticity is a difficult concept to accurately define, but one way to empirically measure it is to use computational methods. Here, Prof. Schleyer describes the “NICS effect” as a method of measuring aromaticity, based on magnetic susceptibility exaltation. Aromatic compounds have a ‘ring current’ due to the conjugation of the p orbitals and the presence of delocalized p electrons, and are therefore diamagnetic. This can be measured experimentally or probed computationally. - The Cyclodecapentaene System
Dr. E. Vogel, Dipl.‐Chem. H. D. Roth
Angew. Chem. Int. Ed. 1964, 3 (3), 228-229
DOI: 10.1002/anie.196402282 - Perspektiven der Cycloheptatrien-Norcaradien-Valenztautomerie
Emanuel Vogel
Pure Appl. Chem. 1969, 20 (3), 237-262
DOI: 10.1351/pac196920030237
The above two papers are on the synthesis and characterization of cyclodeca-1,3,5,7,9-pentaene. The NMR spectrum shows a diamagnetic ring current of the type expected in an aromatic system. - Synthesis of 1,6-didehydro[10]annulene. Observation of its exceptionally facile rearrangement to form the biradical 1,5-dehydronaphthalene
Andrew G. Myers and Nathaniel S. Finney
Journal of the American Chemical Society 1992, 114 (27), 10986-10987
DOI: 10.1021/ja00053a059
Myers (now at Harvard) started his career as a professor at Caltech, and his early papers are gems in physical organic chemistry. This is no exception, and the brevity of this communication belies the extreme difficulty of this experimental work, both in synthesis and characterization. The compound intramolecularly cyclizes via a diradical intermediate at low temperature to naphthalene, and this type of reaction is now known as a “Myers cyclization” after Prof. Myers. - HOMO-AROMATIC STRUCTURES
S. Winstein
Journal of the American Chemical Society 1959, 81 (24), 6524-6525
DOI: 10.1021/ja01533a052
The term ‘homoaromaticity’ was first introduced to chemistry in this paper by organic chemist Prof. Saul Winstein (UCLA). Today, the prefix ‘homo-’ is commonly used in chemistry to denote extension by 1 methylene (-CH2-) group. - UNSATURATED MACROCYCLIC COMPOUNDS. XV.1 CYCLOTETRADECAHEPTAENE
Franz Sondheimer and Yehiel Gaoni
Journal of the American Chemical Society 1960, 82 (21), 5765-5766
DOI: 10.1021/ja01506a061
[14]annulene has been synthesized but found to be unstable even though it has 14 p electrons as per Hückel 4n + 2 p-electron rule. This is because it cannot achieve planarity, thus proving that planarity is an essential criterion for achieving aromatic stabilization! - On the structure and thermochemistry of [18]annulene
Jerome M. Schulman and Raymond L. Disch
Journal of Molecular Structure: THEOCHEM 1991, 234, 213-225
DOI: 10.1016/0166-1280(91)89014-R
[18]annulene is large enough to minimize steric interactions between the internal hydrogens in a geometry that is free of angle strain. The properties of [18]annulene are consistent with its being aromatic. - Ab Initio Density Funtional vs Hartree Fock Predictions for the Structure of [18]Annulene: Evidence for Bond Localization and Diminished Ring Currents in Bicycloannelated [18]Annulenes
Kim K. Baldridge Prof. Jay S. Siegel
Angew. Chem. Int. Ed. 1997, 36 (7), 745-748
DOI: 10.1002/anie.199707451
An stabilization energy of 18 kcal/mol has been calculated for [18]annulene.
I found this page while looking for an answer to why the pyridine ring nitrogen of reduced nicotinamide adenine dinucleotide (NADH) does not become protonated at physiological pH to form NADH2.
I am wondering if the pyridine ring has any partial aromaticity?
And to what extent is that more or less important than steric and electron-withdrawing effects of the ring itself and the nearby ribose?
Thanks for the question! Short answer is that the nitrogen in NADH is very poorly basic here because the lone pair on nitrogen is conjugated with the two adjacent pi bonds. Protonation of these types of functional groups (look up “enamines”) requires pretty strong acid (at least below pH 4). Even if it was protonated at physiological pH, protonation is very reversible, and it would represent a dead-end that just quickly equilibrates back into NADH.
Furthermore, if protonation were to occur, it would happen primarily on carbon, rather than on nitrogen. This is because the nitrogen lone pair donates a lot of electron density into the adjacent alkenes, and these carbons become quite basic (relatively speaking). Enamines protonate primarily on carbon.
There is no partial aromaticity in NADH. The ring in NADH is not aromatic, nor is it even partially aromatic. That’s because the carbon with two H’s attached has no orbital capable of pi-bonding with the adjacent atoms. In order for aromaticity to occur, there must be a continuous ring of atoms capable of pi-bonding. When NADH donates hydride (H-) this breaks one of the C-H bonds, and results in formation of a new C-N pi bond. This allows conjugation of pi bonds all around the ring, and formation of an aromatic ring provides the driving force for this reaction.
I hope this answers your question! James
I hope this answers your question
five pairs of changes.
The special case in note 2 (dihydropyrene) is so interesting! By the way, the ongoing Olympic Games remind me of a compound called “olympicene”, which has 5 rings and many isomers since the extra hydrogen results in a sp3 carbon, pretty much like the case in note 2, but not that symmetric. Considering the 1,H-olympicene, it seems like the sp3 carbon would be surrounded by 4 conjugated rings in a semicircle. This makes me wonder how to define the aromaticity for polycyclic compounds, because the sp3 carbon is also locked in the same plane and the whole structure is still flat. I guess the aromaticity can be a “partial” characteristic for this kind of compounds?
Yes. Molecules can still have aromaticity even if one (or more) atoms is sp3. One of the key characteristics of an aromatic molecule is the existence of a ring current, which you can think of as a cyclic pathway for pi electrons to travel in. So long as this cyclic pathway exists, aromaticity is at least theoretically possible.
very good article so well explained…… so neat and clear… and explanation is next level..
Thanks for the clarification James reg. C2 being more nucleophilic in pyrrole.
Guess this requires a small correction to one of your earlier replies and maybe to the overall text portion too..:)
Pyrrole undergoes electrophilic substitution on C2 (or C5) and not C3 (or C4). Would this not mean that C2(C5) is more nucleophilic than C3(C4)? The substitution at C3 more often than not, occurs only if C2(C5) is already substituted.
Yes. The carbons adjacent to the nitrogens on pyrrole are more nucleophilic.
Article almost delivered everything perfectly.
Got it all ;-)
pls tell why cyclo-pentadiene anion is aromatic????
Think about the rules for aromaticity and work through it. Is it cyclic? conjugated around the outside of the ring? how many pi electrons does it have?
Thank u James although it’s a bit strange as whole molecule is not following huckel rule , neither every atom is conjugated
Well, one ring is aromatic and the other is clearly not. Think of it as a substituted benzene derivative.
Is 1,4 dihydronapthalene aromatic?
Yes, the benzene ring portion is aromatic!
If there is a system of 2 fused rings in which one is fully conjugated but other one has sp3 carbon , so will that structure be considered as aromatic since one ring is aromatic?
Yes. The specific example you gave of 1,4-dihydronaphthalene was helpful!
Thanks a lot james
Should we calculate it for the individual ring every time in case of the isolated systems ??
Yes, calculate it for each isolated system.
What about bi phenyl , how can we say it as aromatic????
Look at each of the two rings individually. Both rings are aromatic.
Hi james ,
Will you please tell me that cyclohex- 1,3diene is aromatic or not???
No, absolutely not.
Hi,
What if the furan’s lone pair electrons like this?
Will there be any changes about aromaticity?
https://hizliresim.com/6CuBRw
Thank you!
Although the furan lone pairs are shown off to each side, that’s more to communicate the fact that furan has two lone pairs rather than to convey an accurate depiction of where its lone pairs are in space. The furan oxygen will be sp2. In the p orbital will be a lone pair of electrons, aligned with the other p-orbitals in the pi system. The other lone pair will be in the same plane of the molecule as the C-H bonds.
Hi,
for cyclopentadienyl carbanion, a comment on rehybridization from sp3 (typical in carbanion species) to sp2 to get some benefits from resonance stabilization since it is adjacent to other sp2 hybridized carbons should be given.
Great job!
Good suggestion. Thanks Ruben!
Nice post, easily understandable, clear and brief. I couldn’t praise just in one word
Glad you found it helpful Sendhan!
So, is fulvene anti-aromatic or non-aromatic? My orgo professor says that it is non-aromatic, but I can’t see why. Is it because the p-orbital on the ch2 outside of the ring does not have good overlap with any of the carbons inside the ring?
Non aromatic. It’s stable and isolable. If it were antiaromatic it would not be isolable. The p orbital on the ch2 outside of the ring is not part of the cyclic array of p orbitals. There will be a VERY significant resonance form for fulvene where that “exo” pi bond is polarized such that the p orbital in the ring has 2 electrons and the p orbital outside the ring has zero (in other words, where that CH2 outside of the ring is a carbocation and the carbon it’s attached to is a carbanion). However this is not enough to make it truly aromatic.
Why is the molecule with the interior sp3 hybridized carbons listed as having 10 pi electrons rather than 14?
you’re right. Fixed!
Hi James, great post! However, I think that the ‘strange case of aromaticity’ molecule has 14 pi electrons (as it has 7 pi bonds), not just 10?
Thanks Dave! Fixed
If you were to have a triangle carbon structure with one lone pair and no double bond; would that still count as aromatic due to resonance? or nonaromatic because you have sp3 before resonance? I have a test tomorrow and am confused in this
You sound like you’re describing the conjugate base of cyclopropane. That’s not aromatic since there are sp3 hybridized carbons.
For the [10]annulene example: in it’s isomer, with the CH2, you say that it allows it to be aromatic because it allows it to be planar. However, isn’t the CH2 sp3 hybridized? And wouldn’t that violate the conjugation and empty p-orbital rule? Thank you!
It’s a special case because of the geometry of the molecule – the ch2 is above the plane where the pi bonds are; the pi bonds are otherwise flat
Hey James, I don’t get it. The Benzene Anion: the Carbon with the LP had 1 electron in a p-orbital prior to getting a negative charge, and then afterwards, you assume that it’s p-electron remains intact but it *gets a lone pair* in the newly occupied orbital? That is just not right then, is it? It can either be that it gets a singular electron in the newly occupied orbital or that its p-Orbital electron is drawn out to the new one.
The lone pair comes from the C-H bond, which is at right angles to the p-orbital
Since 4n+2 causes so much grief among UG students, I tend to use odd number of pi electrons pairs….
Phenyl carbocation is aromatic or non aromatic and why
Where is the empty p orbital in the phenyl carbocation in relation to the pi-system? Therein lies your answer.
Crown ether decalin not mention
It has nothing to do with aromaticity!
Greetings from Brazil!
This article was enough to clear my doubts. Thank you so much. :-)
A pharmacy student.
Great, glad to hear it Matheus!
Can you also explain about anti-aromatic compounds?
Right here: https://www.masterorganicchemistry.com/2017/03/27/antiaromaticity/
Wah! wish i had seen this article 6 months before -_- better late than never :) also in case of pyrrole, i have a query (may be irrelevant though to post it here). In pyrrole out of the distal and proximal carbons (wrt N) which are more electron densed? Also are there any articles that you made on ‘anti aromacity’? couldn’t find here. and thanks again, you are my O-chem last-minute-saviour.
Post on anti-aromaticity here: https://www.masterorganicchemistry.com/2017/03/27/antiaromaticity/
For pyrrole, C-3 is more nucleophilic. That’s a good exam question by the way – see if you can figure out why C-3 is more nucleophilic than C-2.
I’m glad but kind of surprised that you didn’t mention homoaromaticity. Big can o’ worms. Have you deliberately tagged it as “hackles” rule?
Homoaromaticity is the kind of thing that deserves a footnote, since it’s so interesting but probably not required for the average reader. Thanks for the tip about “hackles rule” : – )