Conjugation And Resonance In Organic Chemistry

Conjugation In Organic Chemistry: Definition, Examples, Exploration, and Consequences

This is the first in a series of posts that  cover conjugation, pi systems, molecular orbital theory, dienes, 1,2- and 1,4- additions, the Diels Alder reaction and other pericyclic reactions. We’re going to start by reviewing the basics!

• pi-bonds (π-bonds) are formed by the overlap of two adjacent p-orbitals
• if a p-orbital is present on an atom adjacent to the pi bond, then it can also overlap with the p-orbitals from the pi-bond, provided that it is aligned in the same plane
• This overlap is called conjugation and allows for the de-localization of electrons we call resonance.
• Atoms that can contain a p-orbital include carbocations, atoms bearing lone pairs, atoms that participate in an adjacent pi-bond, and atoms bearing a free radical
• Conjugation of an atom with an adjacent pi-bond will affect its bond lengths and electron distribution
• Conjugation is not possible on the bridgehead atom of many bicyclic molecules, since the p-orbital on the bridgehead cannot properly overlap with p-orbitals on adjacent atoms.

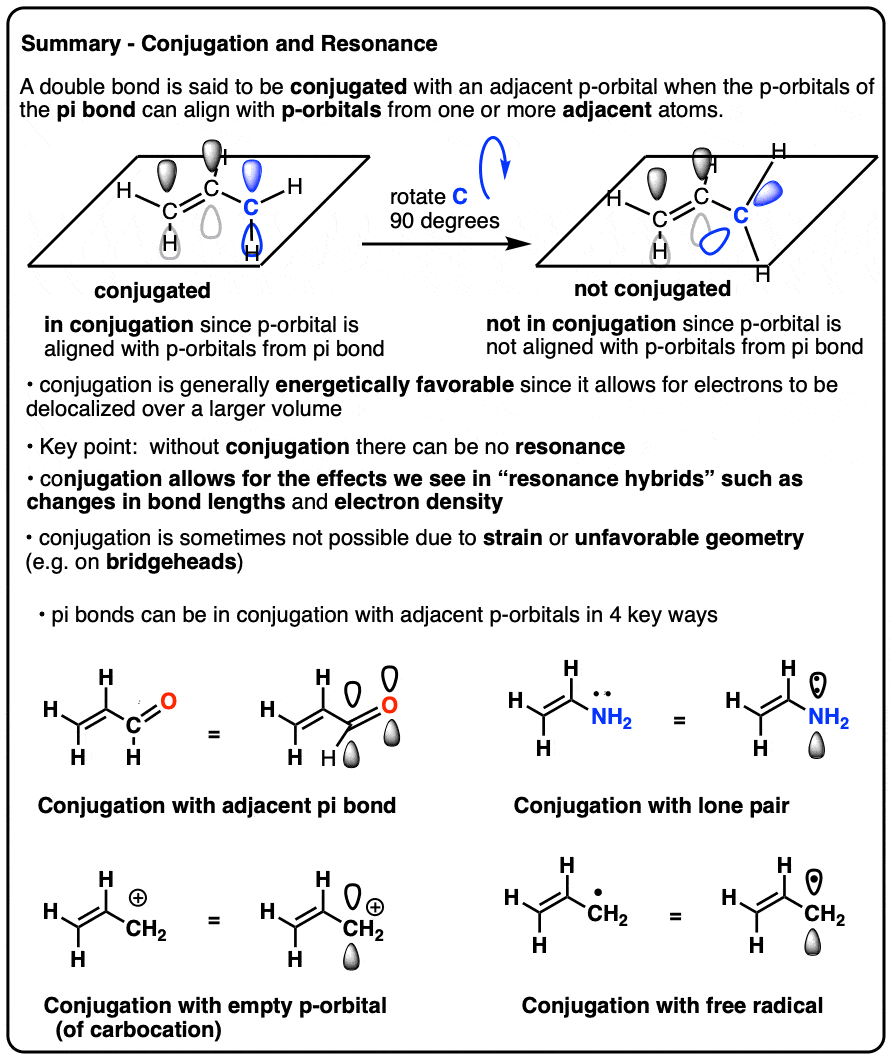
Table of Contents

1. Revisiting the Pi Bond (and Pi bonding): “Side-On” Orbital Overlap Between Adjacent p-Orbitals
2. The Importance Of Orbital Overlap For Pi Bonding
3. Beyond Pi Bonds: “Conjugation” Of 3 Or More p Orbitals
4. The Distinction Between Conjugation And Resonance
5. Consequences of Conjugation (1):  Bond Lengths
6. When Resonance Forms Are Not Identical, The Resonance Hybrid Will Be A “Weighted” Hybrid Of The Most Important Resonance Forms
7. Consequences Of Conjugation (2): “Partial” Double Bonds
8. Consequences of Conjugation (3): The Reactivity Of A Conjugated System Is Often Revealed By Its “Second-Best” Resonance Form
9. Orbital Overlap (All p-Orbitals In The Same Plane) Is Required For Conjugation (And Resonance)
10. Bridgehead Amides Are Not Conjugated, And Are Much More Easily Broken Than “Ordinary” Amides
11. More Consequences Of Conjugation: Color And Cycloadditions
12. Next Up: Molecular Orbital Theory
13. Notes

1. Revisiting the Pi Bond (and Pi bonding): “Side-On” Orbital Overlap Between Adjacent p-Orbitals

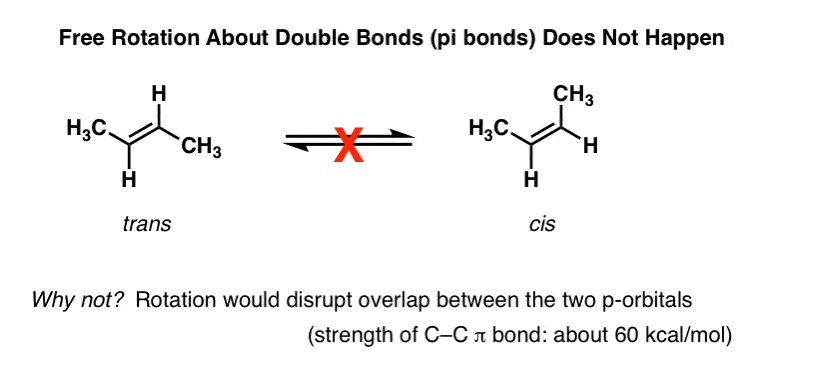
One of the first things you learn about alkenes is that rotation about the C-C pi (π) bond does not occur. For instance, at normal temperatures and pressures., trans-2-butene (shown below left) is never observed to spontaneously convert to cis-2-butene (right) . They’re separable compounds, with different melting and boiling points. You can buy each of them separately from Aldrich. This wouldn’t be possible if there was free rotation about the double bond.

Digging deeper into this, we’ve seen that this is due to a phenomenon called “pi bonding” – a side-on overlap of two adjacent p orbitals, each containing an electron, which results in a preferred orientation where the p-orbitals “line up” next to each other, like soldiers. Due to the dumbbell-like geometry of the p-orbital, overlap isn’t possible when the two p-orbitals are at 90° to each other, which accounts for that “rotational barrier”.

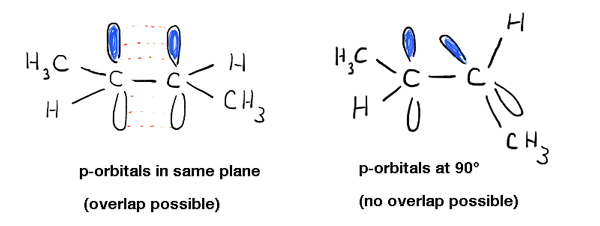
[The shaded (blue) and unshaded (white) lobes of each p-orbital represents a property called “phase”, which is a property of p-orbitals – I’d suggest revisiting this topic if this makes you queasy, because we’ll be using it a lot in the coming posts. As in waves, there is constructive interference between lobes of “like” phase, and destructive interference between lobes of “unlike” phase] 

This has other physical consequences besides the rotation barrier: it influences molecular geometry as well.  Since  Pi-bonding is a phenomenon exclusive to p-orbitals, that means that each pi bond an atom participates in will leave one fewer p-orbital available for “hybridization” with the s orbital [and remaining p orbital(s)] on the atom (See article: Hybrid Orbitals). This results in the familiar “trigonal planar” (sp² ) geometry for typical alkene carbons and “linear” geometry (sp) for alkyne carbons.

Hence, alkenes are “flat”, as opposed to alkyl carbons, which adopt a tetrahedral geometry.

2. The Importance Of Orbital Overlap For Pi Bonding

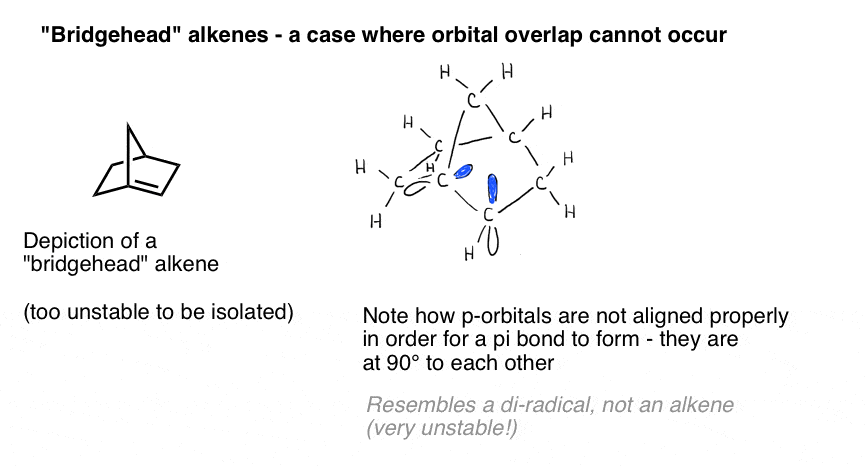
A vivid illustration of the importance of orbital overlap is presented by a case where we might naively think a double bond “should” form – but does not. Bredt observed in 1924 that alkenes tend not to form on “bridgehead” positions, such as in the molecule at bottom left, an observation that came to be called “Bredt’s rule“.

Why not? If you make the model, you’ll see that the geometry of the bicyclic ring forces those p orbitals to be oriented at right angles. There’s no overlap between the p orbitals. Therefore, it resembles a carbon with two adjacent radicals more than it does a real pi bond!

Three dimensional drawings on a flat surface don’t really do justice to glory of the 3-dimensional structure. Here’s a model and accompanying video.  [RIP Vine, which was awesome for short organic chemistry videos]

Those pink things are supposed to be the p-orbitals. See how they’re at right angles to each other? That means they don’t overlap.

via GIPHY

The bottom line is that you need overlap between p orbitals in order for a Pi bond to form. In acyclic systems that’s generally not a problem [see Note 1 for a prominent exception]

3. Beyond Pi Bonds: “Conjugation” Of 3 Or More p Orbitals

In first semester organic chemistry we learn that this overlap of p orbitals is not necessarily confined to two adjacent p orbitals. Overlap can extend beyond two p orbitals to include three, four, five, and even more consecutive p orbitals on consecutive atoms, building larger “pi-systems” (witness lycopene, for instance).

We also see that definition of  “p orbital” is somewhat flexible, and can include examples such as

• an empty p orbital (such as that in a carbocation, or the empty p orbital on boron)
• an orbital containing a lone pair (e.g. on nitrogen, oxygen, fluorine, etc.)
• p-orbitals of a pi bond [such as another alkene, C=O (carbonyl), etc.]
• a half-filled orbital (e.g. a radical)

We call this “building up” of p orbitals into larger “pi systems”,  “conjugation”. In each of the middle molecules below, the alkene (pi bond) is conjugated with an adjacent p orbital.

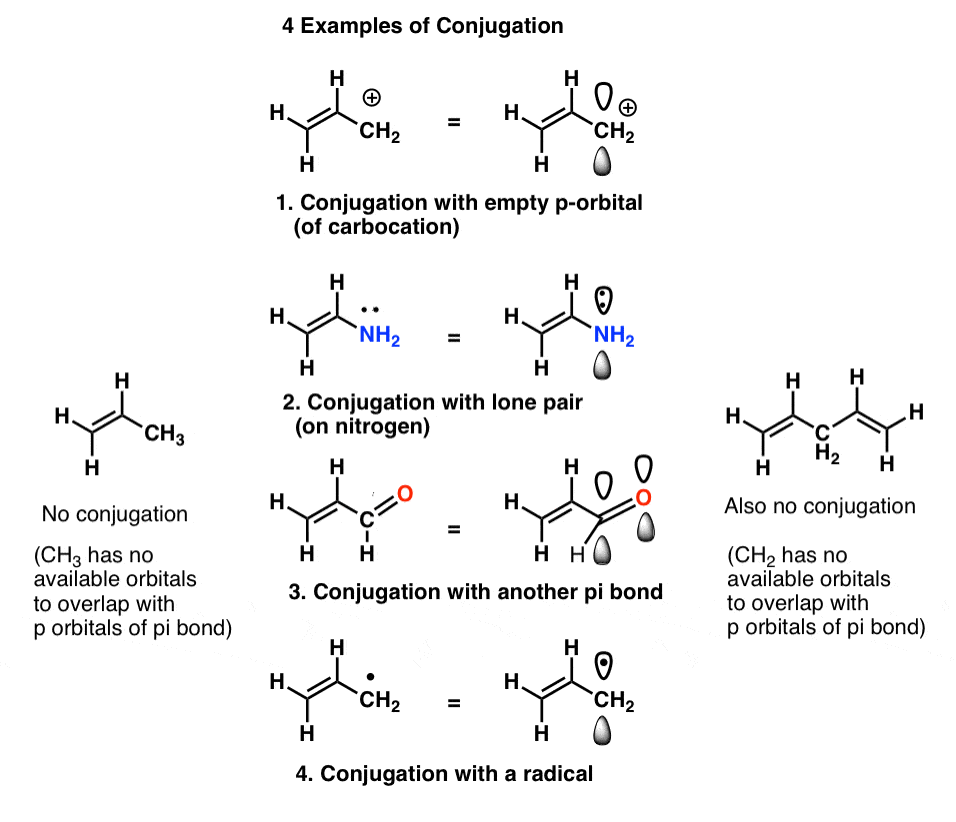
The “conjugation killer” to watch out for is an atom lacking lone pairs connected to only single bonds, such as CH₂ in the example below-right (1,4-pentadiene). These two pi bonds are not conjugated.

[A note on the second example. We usually think of the geometry of a nitrogen with three single bonds as trigonal pyramidal (e.g. as in NH₃). But in the presence of an adjacent pi bond, there is a slight “re-hybridization” of the nitrogen from sp³ to sp² (trigonal planar) such that the lone pair is in a p orbital, not an sp³ orbital.  This is a tradeoff:  the slightly increased strain of the eclipsed N-H bonds is made up for by a decrease in overall energy due to better overlap of a p orbital with the pi bond. We usually think of this as “resonance energy“.]

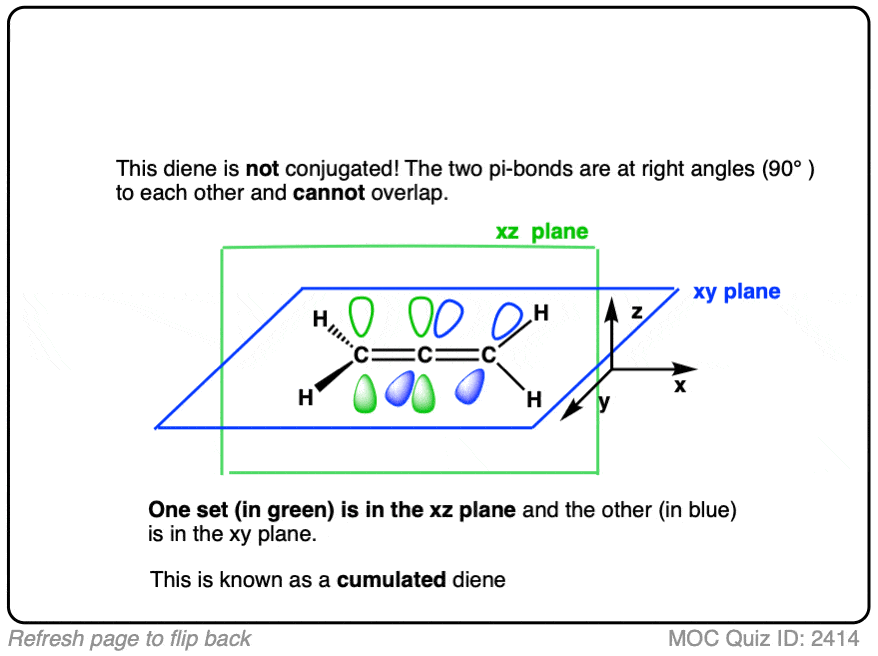
Here’s a fun  trick question. Are the the double bonds in the molecule below (allene) conjugated? Why or why not?

4. The Distinction Between Conjugation And Resonance

You might well ask: this just sounds like resonance. What’s the difference?

Let’s take a second to distinguish conjugation and resonance.

• Conjugation is what we call it when 3 or more p orbitals join together into a larger “pi system”.
• These conjugated pi systems contain electrons, which we often call “pi electrons” to distinguish them from the electrons that comprise single bonds in the molecule.
• The different arrangements of electrons within that “pi system” are called resonance forms.

A rough analogy could go like this:

• Think of p orbitals as being a bit like “rooms” for electrons (maximum occupancy: 2)
• Joining several rooms together into a larger building is conjugation
• The different allowable arrangements of people (electrons) within that building are resonance forms.

The key requirement for conjugation is orbital overlap, which we’ll expand on in a bit.

For now, let’s review some consequences of conjugation.

5. Consequences of Conjugation (1):  Bond Lengths 

As I just said, we’re more used to conjugation in the context of “resonance“, a concept we’ve covered before (and since this series is going into second-semester territory, is worth re-familiarizing yourself with)

For instance, with the acetate ion (CH₃CO₂)^–  and the allyl cation (both shown below), we saw that there’s two different ways of arranging the pi electrons, which we call “resonance forms”.

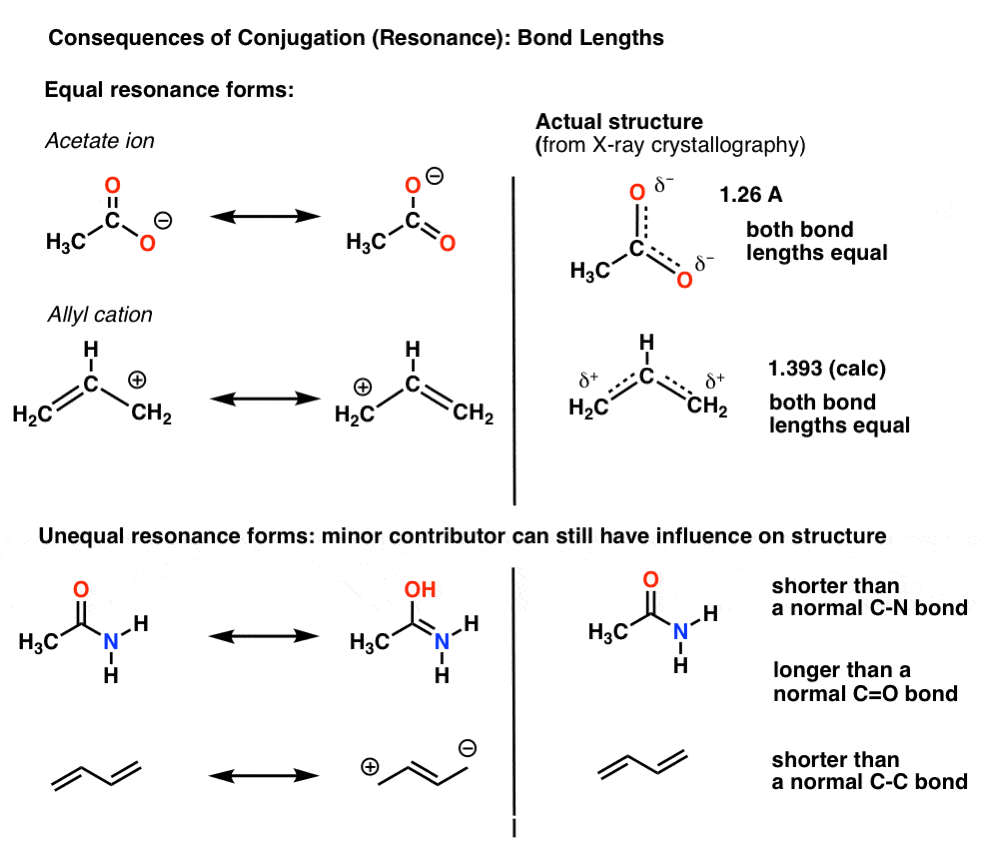
The important point to note is that the pi-electrons in these are not constantly switching back-and-forth between atoms; rather, the “true” structure of the molecule is a hybrid of these resonance forms.

One important consequence of resonance is bond lengths that are intermediate between two forms. 

For example, the C-O bond length in the acetate ion (1.26 Å)  is between what we’d expect for a C-O pi bond (1.20 Å) and a C-O single bond (1.4 Å). 

6. When Resonance Forms Are Not Identical, The Resonance Hybrid Will Be A “Weighted” Hybrid Of The Most Important Resonance Forms

In the acetate ion and the allyl cation the two important resonance forms are equivalent, so both end up contributing equally to the hybrid.

A more common situation is found molecules like the ones below there’s a blending of unequal resonance forms. Some resonance forms are more important than others. [to go back to determining how to evaluate resonance forms, go to this series of posts. ].

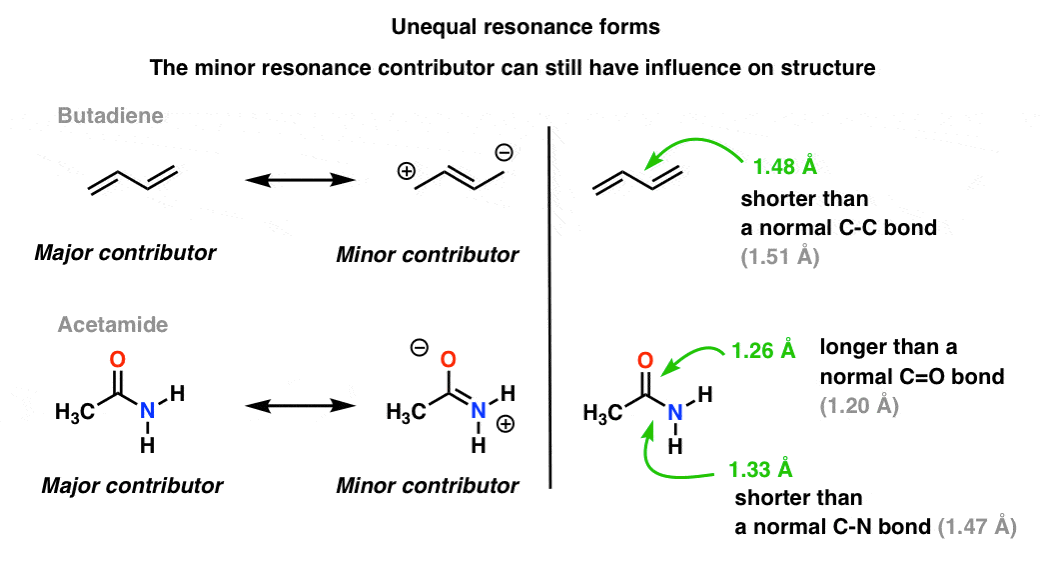
Our visual language of chemistry with its sharp distinction between single and double bonds does not accurately depict the electron density in the molecules, which are a weighted hybrid of resonance forms. Minor resonance contributors influence the bond lengths in the molecule, making them shorter or longer than normal.

In the top molecule (butadiene), that central C-C bond is a little bit shorter than a “normal” C-C single bond (i.e. it has a bit of double bond character) due to the influence of the minor resonance contributor to the hybrid. [Note that the bond length is not halfway between single and double C-C bond, as it was in the allyl cation: that’s because the two resonance forms are not equally important (i.e. do not make equal contributions to the resonance hybrid)] 

In the bottom molecule (“acetamide”) the C-O bond is a little bit longer than a “normal” C=O bond (i.e. has more single-bond character) and the C-N bond is a little bit shorter than a “normal” C-N bond (i.e. has more double-bond character). This reflects the influence of the “minor contributor” (or “second best” contributor, if you like) in which there is a C-N pi bond and a C-O single bond.

Let’s make our first conceptual leap.

7. Consequences Of Conjugation (2): “Partial” Double Bonds

There’s an interesting consequence of that “partial double bond character” in the C-N bond. It has a “barrier to rotation” just like we’d expect from a “double bond”!  The barrier to rotation in the C-N bond of amides is about 15-20 kcal/mol in peptide bonds (compare to about 2-3 kcal/mol for most C-C bonds).

What this means is that the two conformations can still interconvert, but they do so relatively slowly at room temperature. In the molecule below (N-methyl acetamide)  it’s possible to observe the s-cis conformer (both green methyl groups on the same side of the C-N bond) and the s-trans conformer (green methyl groups on opposite sides of the C-N bond) separately. [Note 4] This usually isn’t possible for conformers unless you take the temperature down to 100 Kelvin or so!

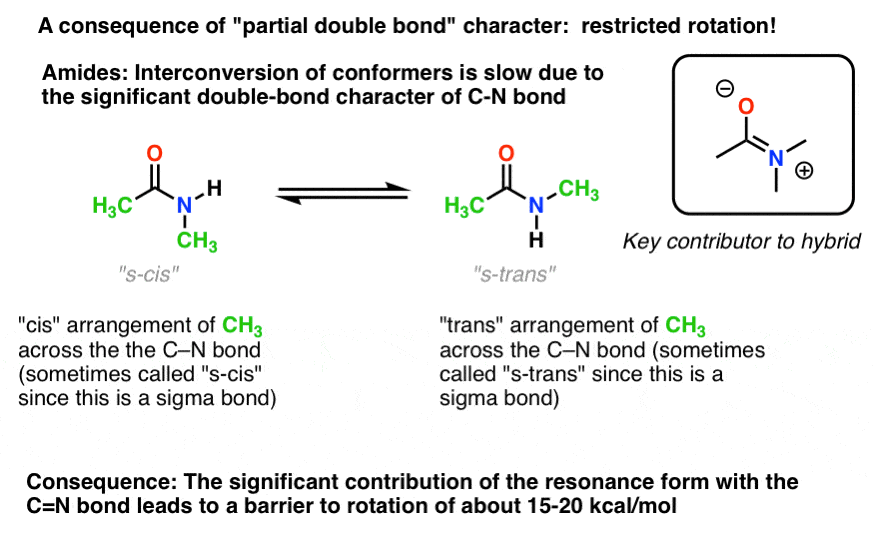
For the image above, the crucial concept here is just the partial double bond character. If s-cis and s-trans doesn’t make sense to you after thinking about it for a bit, it’s OK. Not crucial for the rest of the discussion.

8. Consequences of Conjugation (3): The Reactivity Of A Conjugated System Is Often Revealed By Its “Second-Best” Resonance Form

We’ve shown the effect that conjugation (and by extension, resonance) has on bond lengths.

Let’s take a closer look at its effect on electron density, which ultimately influences reactivity.

For illustrative purposes, let’s continue to look at alkenes.

The reactivity of an alkene can be modified dramatically through the attachment of various groups.

Look at the “second best” resonance form when we attach a  pi-donor such as N(CH₃)₂ to an alkene. This results in a build-up of negative charge (δ^–) on terminal carbon of the alkene, with the result that this alkene (which we call an enamine) is an excellent nucleophile. To take just one prominent example, enamines react with alkyl halides (such as CH₃I) and other electrophiles in a class of reactions sometimes referred to as Stork Enamine reactions after their discoverer, Gilbert Stork.  Ordinary alkenes such as 2-butene (below) don’t work in this reaction.

Attachment of a pi-acceptor such as C=O results in a  build-up of positive charge (δ⁺) on the terminal carbon of the alkene, with the result that this species (which we call an α, β unsaturated aldehyde, Michael acceptor, or enone) is an excellent electrophile. α, β  unsaturated carbonyls react with nucleophiles (such as CH₃S^–) and many other classes of nucleophiles in a general type of reaction we call conjugate additions or sometimes Michael reactions.

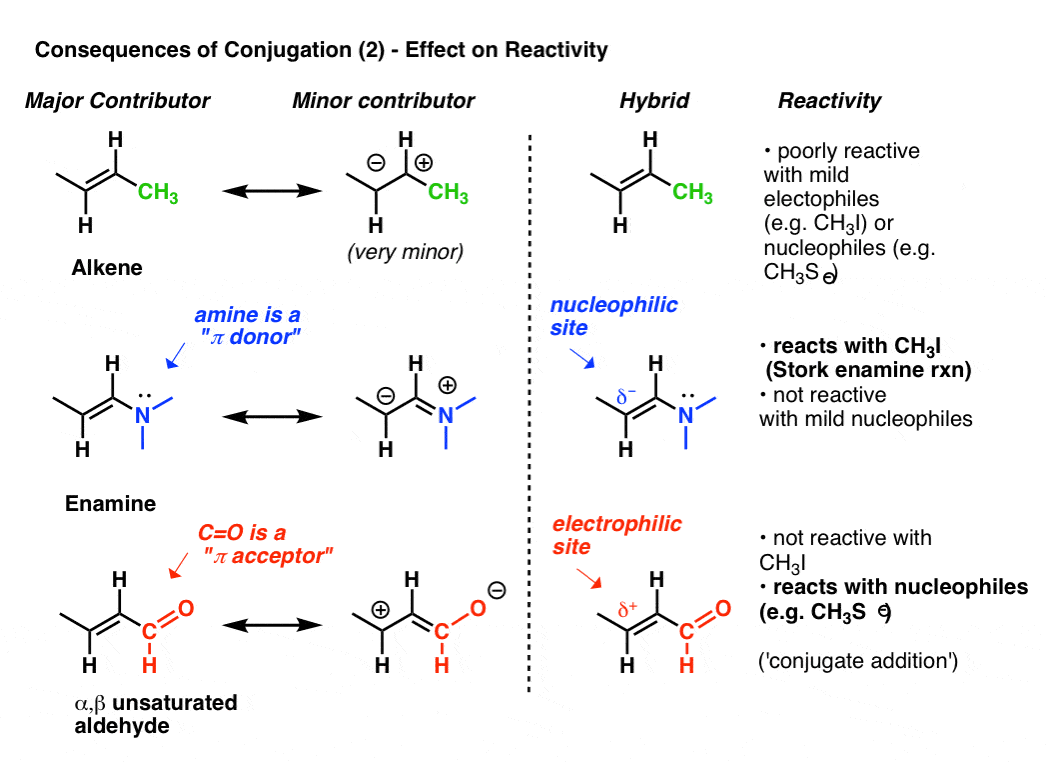
This is just the tip of the iceberg as to how conjugation can affect reactivity, but it’s enough for today.

9. Orbital Overlap (All p-Orbitals In The Same Plane) Is Required For Conjugation (And Resonance)

So far we’ve seen that:

• overlap between p orbitals is necessary to form pi bonds
• some “single bonds” can have “pi bond character” due to contribution from a minor resonance form (such as amides, for example)

Here is the logical consequence of these two statements:

• In order for conjugation to exist, and therefore in order for resonance to occur, all the p orbitals must overlap. They must therefore all be aligned in the same plane.

Remember the “allyl cation” that is “stabilized by resonance”? In order for the carbocation to gain this “resonance stabilization”, the empty p orbital on the carbocation must be lined up with the adjacent pi bond.

If the p orbital is at an angle of 90 degrees from the p orbitals in the pi bond, there is no conjugation and thus no resonance stabilization.

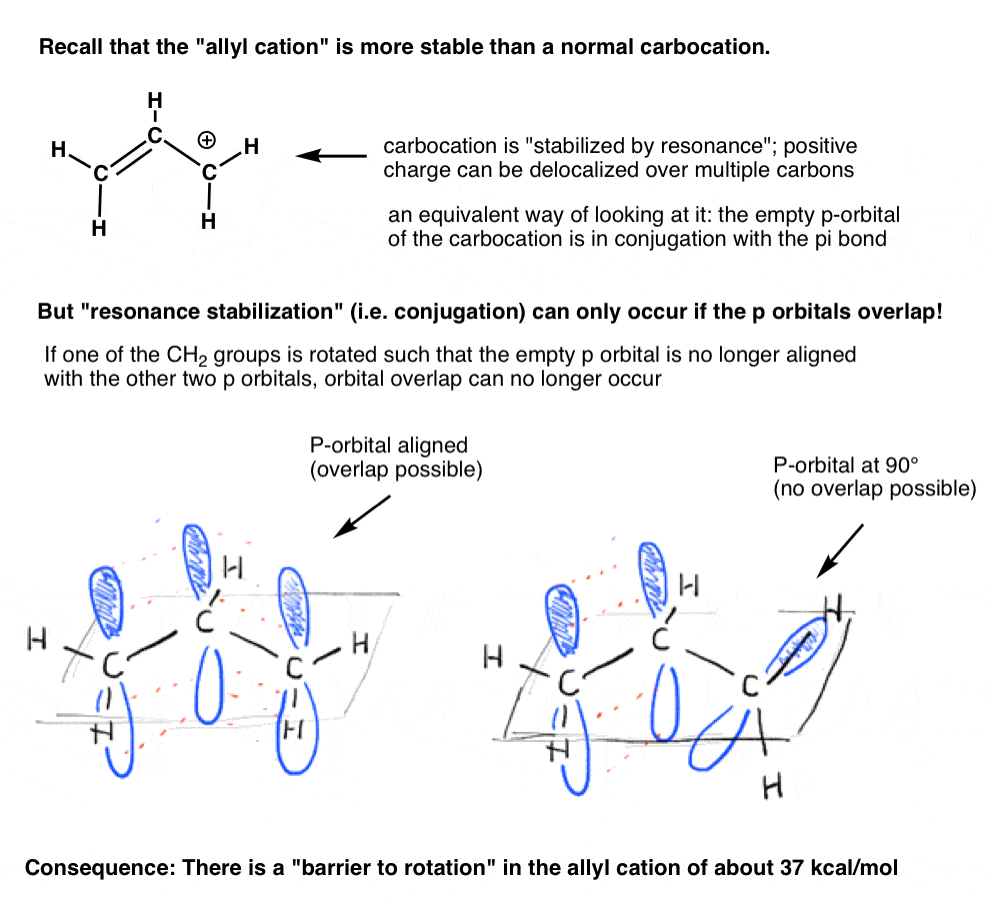
As we might predict, there is a barrier to rotation in the allyl cation, just as there is a barrier to rotation in an alkene. The barrier to rotation in the allyl cation is about 37 kcal/mol – a little more than half the strength of a C-C pi bond.

We also saw that the C-N bond in amides has partial double bond character, with a barrier to rotation of about 15-20 kcal/mol.

Likewise, this “partial double bond” character is only possible if the p orbital containing the lone pair is able to overlap with the p orbitals comprising the C=O pi bond.

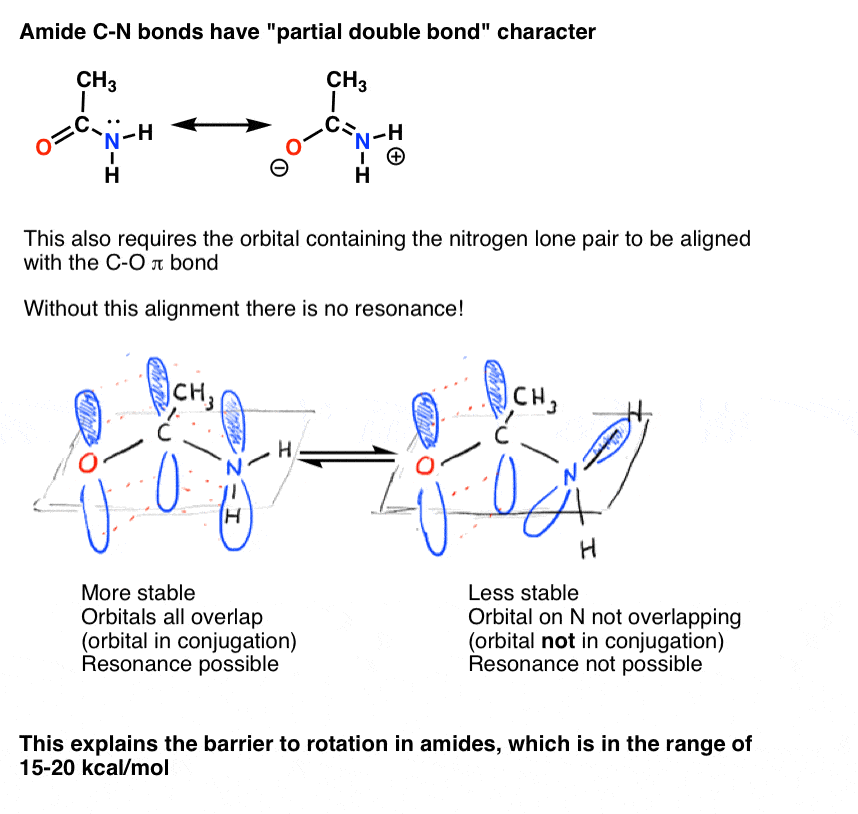
The partial double bond character of the C-N bond in amides has long been thought to be the main reason why they are much more resistant to breakage than, say, esters [for an advanced treatment, see Note 2]. Since the proteins in our body are joined by peptide (amide) linkages, this is a matter of no small importance! Life-forms based on ester rather than amide linkages would be much more fragile!

10. Bridgehead Amides Are Not Conjugated, And Are Much More Easily Broken Than “Ordinary” Amides

Bridgehead amides give an illustration of what happens to amides when overlap is impossible.

Just as we saw in bridgehead alkenes, in bridgehead amides, orbital overlap between the nitrogen lone pair and carbonyl carbon is impossible due to twisting. The result is that the C-N bond does NOT have partial double bond character and it is much easier to break than a “normal” amide.

The bridgehead amide below is “quinuclidone”, a twisted amide that eluded synthesis for decades. It was only in 2006 that it was finally made (as its conjugate acid) through a clever route by the lab of Brian Stoltz at Caltech.

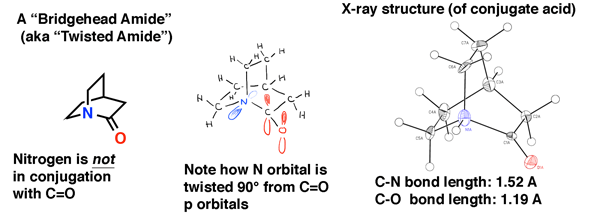
The X-ray crystal structure bears witness to the lack of conjugation in this amide. The C-N bond length is 1.52 Å (typical of a single C-N bond) and the C=O bond length is 1.19 Å, which is typical of a bond length in an aldehyde or ketone (1.20 Å). We would therefore expect that it is quite a bit more unstable towards nucleophilic attack than a normal amide, which was borne out in the Stoltz lab’s study.

Here’s a 3-D model of quinuclidine (courtesy of Rowan). The lone pair on nitrogen is not visible here, but just like the bridgehead C-H bond, it points straight out from the bridgehead and cannot overlap with the C-O pi bond.

11. More Consequences Of Conjugation: Color And Cycloadditions

So far, this post has pretty much been a review of 1st semester concepts.  There’s nothing in the discussion above that couldn’t be reasonably explained by what we’ve already learned about conjugation and resonance.

However, this simplistic approach can only take us so far.

Two quick examples, because this post has gone on long enough.

First: Conjugation And Color

If you saw this post on how bleach works, you learned that as we lengthen the conjugation length, we change the wavelength at which molecules absorb light. Some very brightly coloured molecules such as carotene, chlorophyll and lycopene all have very long conjugated double bonds.

For instance, lycopene is responsible for the red colour of tomatoes. If we remove the double bonds, we remove the colour. Why?

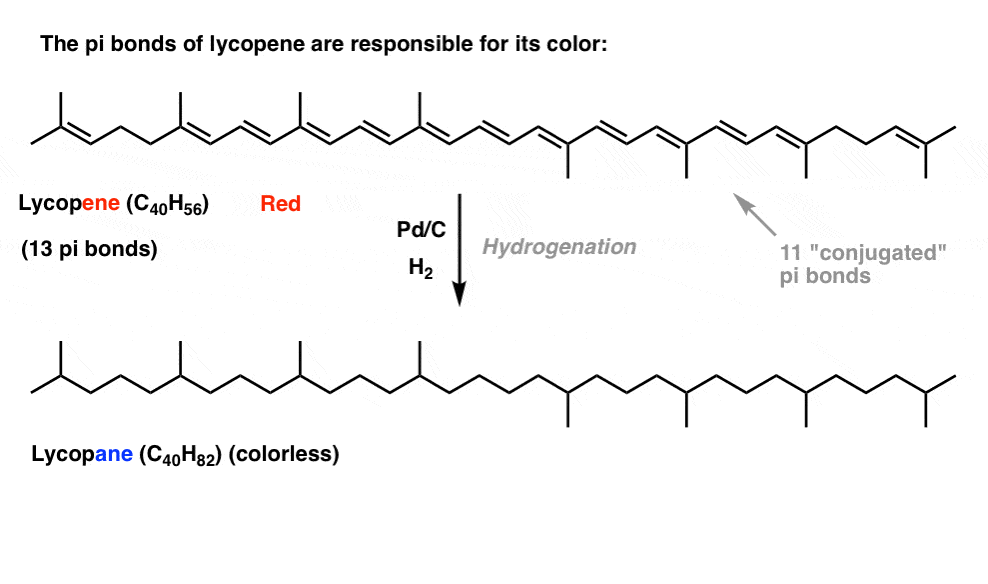
What’s the relationship between color and conjugation? Why would the number of double bonds have an influence on this? Resonance fails to illuminate this subject.

Second: Reactions of Dienes That Form Rings

Here’s some weird reactions for you.

If you treat butadiene with the molecule to its right (methyl maleate) you obtain a new product containing a six membered ring. Nothing we’ve seen so far prepares us for this type of reaction, which is called a “cycloaddition”.

Interestingly, if you treat ethene with the same molecule, nothing happens (except if you treat it with UV light. Then you get a 4-membered ring, but I digress). 

WHY?

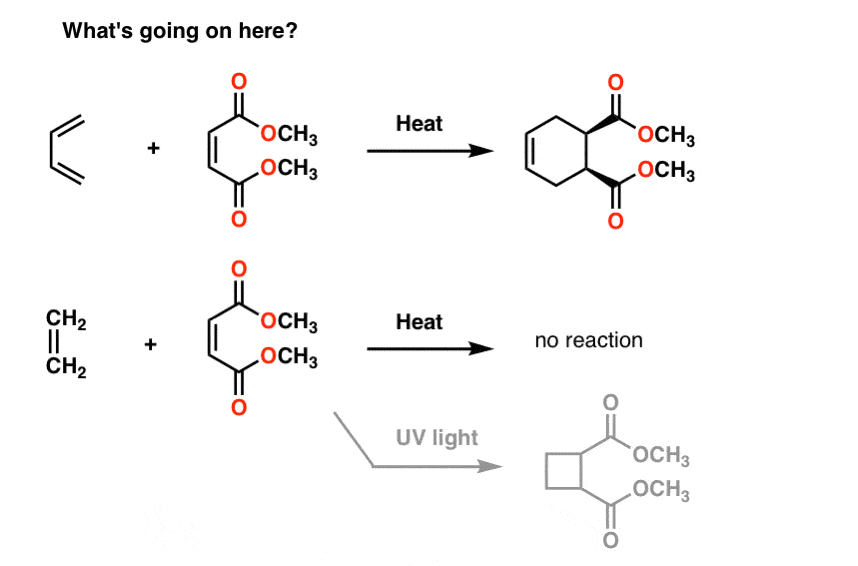
Resonance doesn’t help us here either.

12. Next Up: Molecular Orbital Theory

What will help us answer these questions, as well as many others going forward is a concept called molecular orbital theory. 

In the following posts in this series, we’re going to dig more deeply into how p orbitals overlap to form molecular orbitals, and we’ll examine the energy levels of these orbitals. We’ll also see how this influences the reactivity of molecules and allows us to make predictions about their chemical behaviour.

As we’ll see, molecular orbital theory provides us with a very powerful set of concepts that will help us understand chemical reactivity at a much deeper level.

Thanks to Tom Struble for all his help with this post. 

Notes

 Note 1. A-1,2 strain is the reason why tetra-tert-butylethylene has not yet been synthesized.

Note 2. The pi bonds are not conjugated. Look at the orbitals comprising the two pi bonds. They are at right angles to each other and cannot overlap.

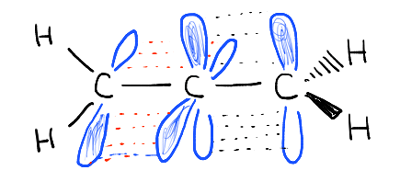
Note 3. recent work suggests that resonance is not as important in amide bond restriction as was thought previously. See here (Modern Physical Organic Chemistry by Anslyn and Dougherty, p. 23)]

Note 4. Using NMR, nuclear magnetic resonance spectroscopy. These conformational isomers are sometimes called “rotational isomers” or “rotamers” and they can complicate NMR spectra considerably. The peaks can usually be made to coalesce by heating the sample probe.

This stands in contrast to, say, different chair forms of cyclohexane, which generally can still interconvert at room temperature and coalesce to a single peak. However if you cool a substituted cyclohexane enough you can “freeze out” the different conformers and observe them separately.